《2025年学考A加同步课时练九年级数学下册人教版》

5. 如图，矩形OABC的顶点A，C分别在x轴和y轴上，点B的坐标为(2，3)，双曲线y = $\frac{k}{x}$(x＞0)经过BC上的点D与AB交于点E，连接DE，若E是AB的中点.
(1)求D点的坐标；
(2)点F是OC边上一点，若△FBC和△DEB相似，求直线BF的解析式.

答案： 解:
(1)
∵四边形ABCD是矩形，
∴OA=BC,AB=OC.
∵B(2,3),E为AB的中点,
∴AB=OC=3,
　OA=BC=2,AE=BE=$\frac{1}{2}$AB=$\frac{3}{2}$,
∴E(2,$\frac{3}{2}$),
∴k=2×$\frac{3}{2}$=3,
∴双曲线的解析式为y=$\frac{3}{x}$.
∵点D在双曲线y=$\frac{3}{x}$(x＞0)上,
∴OC·CD=3,
∴CD=1,
∴点D的坐标为(1,3).
(2)
∵BC=2,CD=1,
∴BD=$\sqrt{BC^{2}+CD^{2}}=\sqrt{2^{2}+1^{2}}=\sqrt{5}$.
分两种情况:
　①当△FBC和△DEB相似，BD和BC是对应边时，$\frac{BD}{BE}=\frac{BC}{CF}$,即$\frac{\sqrt{5}}{\frac{3}{2}}=\frac{2}{CF}$,
∴CF=$\frac{3}{\sqrt{5}}=\frac{3\sqrt{5}}{5}$,
∴F(0,0),即点F与点O重合
　设直线BF的解析式为y=mx,把点B(2,3)代入得m=$\frac{3}{2}$,
∴直线BF的解析式为y=$\frac{3}{2}$x;
　②当△FBC和△DEB相似，BD与CF是对应边时，$\frac{BD}{BE}=\frac{CF}{BC}$,即$\frac{\sqrt{5}}{\frac{3}{2}}=\frac{CF}{2}$
∴CF=$\frac{4\sqrt{5}}{5}$,
∴OF=3−$\frac{4\sqrt{5}}{5}$,
∴F(0,3 - $\frac{4\sqrt{5}}{5}$).设直线BF的解析式为y=nx + c,
　把B(2,3),F(0,3 - $\frac{4\sqrt{5}}{5}$)代入得$\begin{cases}2n + c = 3\\c = 3 - \frac{4\sqrt{5}}{5}\end{cases}$,
　解得n=$\frac{2\sqrt{5}}{5}$,c=$3 - \frac{4\sqrt{5}}{5}$,
∴直线BF的解析式为y=$\frac{2\sqrt{5}}{5}$x+3 - $\frac{4\sqrt{5}}{5}$.
　综上所述，若△FBC和△DEB相似,BF的解析式为y=$\frac{3}{2}$x或y=$\frac{2\sqrt{5}}{5}$x+3 - $\frac{4\sqrt{5}}{5}$.

6. 一块材料的形状是锐角三角形ABC，边BC = 120mm，高AD = 80mm，把它加工成正方形零件如图①，使正方形的一边在BC上，其余两个顶点分别在AB，AC上.
(1)求证：△AEF∽△ABC；
(2)求这个正方形零件的边长；
(3)如果把它加工成矩形零件如图②，这个矩形的最大面积是多少?

答案： 解:
(1)证明:
∵四边形EGHF为正方形，
∴BC//EF,
∴△AEF∽△ABC.
(2)设正方形零件的边长为xmm,则KD=EF =x,AK=80−x,
∵EF//BC,
∴△AEF∽△ABC;
∵AD⊥BC,
∴$\frac{EF}{BC}=\frac{AK}{AD}$,
∴$\frac{x}{120}=\frac{80−x}{80}$,解得x=48.
　所以正方形零件的边长为48mm.
(3)设EF=x,EG=y,
　由
(2)可知$\frac{EF}{BC}=\frac{AK}{AD}$,
∴$\frac{x}{120}=\frac{80 - y}{80}$,
∴y=80−$\frac{2}{3}$x.
∴矩形面积S=xy=−$\frac{2}{3}$x²+80x=−$\frac{2}{3}$(x−60)²+2400(0＜x＜120).
　故当x=60时，矩形的面积最大，最大面积为2400mm².

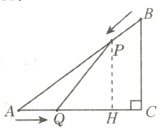
7. 如图所示，在△ABC中，∠ACB = 90°，AC = 4cm，BC = 3cm，点P由点B出发，沿BA方向向点A匀速运动，同时点Q由点A出发，沿AC方向向点C匀速运动，它们的速度均为1cm/s. 连接PQ，设运动时间为t s(0＜t＜4).
(1)当t为何值时，PQ⊥AC?
(2)设△APQ的面积为S，求S关于t的函数解析式，并求出当t为何值时，S取得最大值? S的最大值是多少?

答案：
解:
(1)
∵PQ⊥AC,
∴∠AQP=∠C=90°
∴PQ//BC,
∴$\frac{AP}{AB}=\frac{AQ}{AC}$
　在Rt△ACB中,
　AB=$\sqrt{AC^{2}+BC^{2}}=\sqrt{4^{2}+3^{2}}=5$,
∴$\frac{5 - t}{5}=\frac{t}{4}$,解得t=$\frac{20}{9}$
∴当t为$\frac{20}{9}$时,PQ⊥AC;
(2)如图，作PH⊥AC于点H.
∵PH//BC,
∴$\frac{PA}{AB}=\frac{PH}{BC}$,
∴$\frac{5 - t}{5}=\frac{PH}{3}$,
　
∴PH=$\frac{3}{5}$(5 - t),
∴S=$\frac{1}{2}$AQ·PH=$\frac{1}{2}t\times\frac{3}{5}$(5 - t)=−$\frac{3}{10}t^{2}+\frac{3}{2}t=−\frac{3}{10}(t - \frac{5}{2})^{2}+\frac{15}{8}$.
∵$-\frac{3}{10}$＜0,
∴当t=$\frac{5}{2}$时,S有最大值，最大值为$\frac{15}{8}$.