《2025年学考A加同步课时练九年级数学下册人教版》

1. 如图，在△ABC中，∠C = 90°，AC = 3，BC = 4，P为BC边上的动点(与点B，C不重合)，PD//AB，交AC于点D，连接AP，设CP = x，△ADP的面积为S.
(1)用含x的代数式表示AD的长；
(2)求S关于x的函数解析式，并求当S随x增大而减小时x的取值范围.

答案： 解:
(1)
∵PD//AB,
∴$\frac{CD}{CB}=\frac{CP}{CA}$.
∵AC=3,BC=4,CP=x,
∴$\frac{x}{4}=\frac{CD}{3}$,
∴CD=$\frac{3}{4}$x,
∴AD=AC−CD=3−$\frac{3}{4}$x,
　即AD=−$\frac{3}{4}$x+3.
(2)根据题意，得S=$\frac{1}{2}$AD·CP=
　$\frac{1}{2}$x(−$\frac{3}{4}$x+3)=−$\frac{3}{8}$(x−2)²+$\frac{3}{2}$,
∴当x≥2时,S随x的增大而减小
∵0＜x＜4,
∴当S随x增大而减小时x的取值范围为2≤x＜4.

2. 在△ABC中，AB = 6，AC = 8，点D，E分别在AB，AC上，连接DE，设BD = x(0＜x＜6)，CE = y(0＜y＜8).
(1)当x = 2，y = 5时，求证：△AED∽△ABC；
(2)若△ADE和△ABC相似，求y关于x的函数解析式.

答案：
(1)证明:
∵AB=6,BD=2,
∴AD=4.
∵AC=8,CE=5,
∴AE=3,
∴$\frac{AE}{AB}=\frac{3}{6}=\frac{1}{2}$,$\frac{AD}{AC}=\frac{4}{8}=\frac{1}{2}$,
∴$\frac{AE}{AB}=\frac{AD}{AC}$.
∵∠EAD=∠BAC,
∴△AED∽△ABC.
(2)解:①若△ADE∽△ABC,则$\frac{6 - x}{6}=\frac{8 - y}{8}$,
∴y=$\frac{4}{3}$x(0＜x＜6).
　②若△ADE∽△ACB,则$\frac{6 - x}{8}=\frac{8 - y}{6}$,
∴y=$\frac{3}{4}$x+$\frac{7}{2}$(0＜x＜6).

3. 如图，等腰三角形ABC中，AC = BC = 8，点D，E分别是边AB，BC上一动点(不与顶点重合)，且∠CDE = ∠A，CE = 5，设AD = x，BD = y.
(1)求y关于x的函数解析式(不用写出x的取值范围)；
(2)当AB = 10时，求$\frac{CD}{DE}$的值.

答案： 解:
(1)
∵AC=BC=8,CE=5,
∴∠A=∠B,BE=3.
∵∠BDC=∠A+∠ACD,
　即∠BDE+∠CDE=∠A+∠ACD,
　且∠CDE=∠A,
∴∠BDE = ∠ACD,
∴△ACD∽△BDE,
∴$\frac{AC}{BD}=\frac{AD}{BE}$,即$\frac{8}{x}=\frac{y}{3}$,则$y=\frac{24}{x}$.
(2)
∵AB=10,即x+y=10,xy=24,
∴x=4,y=6或x=6,y=4,
　则BD=6或4.
∵△ACD∽△BDE,
∴$\frac{CD}{DE}=\frac{AC}{BD}$,
∴$\frac{CD}{DE}=\frac{8}{6}=\frac{4}{3}$或$\frac{CD}{DE}=\frac{8}{4}=2$.

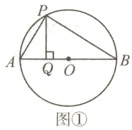
4. (1)如图①，AB为⊙O的直径，点P在⊙O上，过点P作PQ⊥AB，垂足为点Q. 说明△APQ∽△ABP；
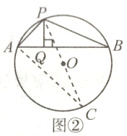
(2)如图②，⊙O的半径为7，点P在⊙O上，点Q在⊙O内，且PQ = 4，过点Q作PQ的垂线交⊙O于点A，B. 设PA = x，PB = y，求y关于x的函数解析式.

答案：
解:
(1)如图①所示，
∵AB为⊙O的直径，
∴∠APB=90°.
　又
∵PQ⊥AB,
∴∠AQP=90°.
∴∠AQP=∠APB.
　
　又
∵∠PAQ=∠BAP,
∴△APQ∽△ABP.
(2)如图②,连接PO,并延长
　PO交⊙O于点C,连接AC;
∵PC为⊙O的直径，
∴∠PAC=90°,
　又
∵PQ⊥AB,
∴∠PQB=90°,
∴∠PAC=∠PQB.
　
　又
∵∠C=∠B(同弧所对的圆周角),
∴△PAC∽△PQB,
∴$\frac{PA}{PQ}=\frac{PC}{PB}$
　又
∵⊙O的半径为7,即PC=14,
　且PQ=4,PA=x,PB=y,