《2025年学考A加同步课时练九年级数学下册人教版》

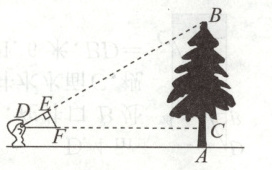
6. 如图，一位同学通过调整自己的位置，设法使三角板DEF的斜边DF保持水平，并且边DE与点B在同一直线上，已知DE = 0.4m，EF = 0.2m，测得边DF离地面的高度AC = 1.5m，CD = 8m，则树高AB为________m.

答案： 5.5 [解析]
∵∠DEF = ∠DCB = 90°，∠D = ∠D，
∴△DEF∽△DCB，
∴$\frac{DE}{DC}$=$\frac{EF}{CB}$
∵DE = 0.4m，EF = 0.2m，CD = 8m，
∴$\frac{0.4}{8}$=$\frac{0.2}{BC}$，解得BC = 4m，
∴AB = AC + BC = 1.5 + 4 = 5.5(m).
故答案为5.5.

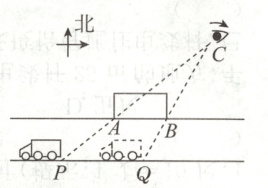
7. 20世纪90年代以来，我国户外广告行业取得了突飞猛进的发展，户外广告装置多设立于城市道路、铁路、公路等主要交通干道边上，面向密集的车流和人流. 某天，小芳走到如图所示的C处时，看到正对面一条东西走向的笔直公路上有一辆汽车从东面驶来，到达Q处时，恰好被公路北侧边上竖着的一个长12m的广告牌AB挡住，3s后在P处又重新看到该汽车的全部车身，已知该汽车的行驶速度是21.6km/h，假设AB//PQ，公路宽为10m，求小芳所在C处到公路南侧PQ的距离.

答案： 解:设小芳所在C处到公路南侧PQ的距离为xm，21.6km/h = 6m/s，
∵AB//PQ，
∴△CAB∽△CPQ，
∴$\frac{AB}{PQ}$=$\frac{x - 10}{x}$，
∴$\frac{12}{6×3}$=$\frac{x - 10}{x}$，
∴x = 30，
∴小芳所在C处到公路南侧PQ的距离为30m.

8. 《九章算术》是中国传统数学最重要的著作，在“勾股”章中有这样一个问题:“今有邑方二百步，各中开门，出东门十五步有木，问:出南门几步而见木？”用今天的话说，大意是:如图，四边形DEFG是一座边长为200步（“步”是古代的长度单位）的正方形小城，东门H位于GD的中点，南门K位于ED的中点，出东门15步的A处有一树木，求出南门多少步恰好看到位于A处的树木（即点D在直线AC上）？请你计算KC的长为多少步.

答案： 解:DH = 100，DK = 100，AH = 15，
∵AH//DK，
∴∠CDK = ∠A，
∴△CDK∽△DAH，
∴$\frac{CK}{DH}$=$\frac{DK}{AH}$，即$\frac{CK}{100}$=$\frac{100}{15}$，
∴CK = $\frac{2000}{3}$.
答:KC的长为$\frac{2000}{3}$步.

9. 大雁塔是现存最早、规模最大的唐代四方楼阁式砖塔，被国务院批准列入第一批全国重点文物保护单位. 某校社会实践小组为了测量大雁塔的高度，在地面上C处垂直于地面竖立了高度为2米的标杆CD，这时地面上的点E，标杆的顶端点D，古塔的塔尖点B正好在同一直线上，测得EC = 1.28米，将标杆向后平移到点G处，这时地面上的点F，标杆的顶端点H，古塔的塔尖点B正好在同一直线上（点F，G，E，C与古塔底处的点A在同一直线上），这时测得FG = 1.92米，CG = 20米，请你根据以上数据，计算古塔的高度AB.

答案： 解:根据题意，得△EDC∽△EBA，△FHG∽△FBA，
∴$\frac{DC}{BA}$=$\frac{EC}{EA}$，$\frac{GH}{AB}$=$\frac{FG}{FA}$.
∵DC = HG，
∴$\frac{FG}{FA}$=$\frac{EC}{EA}$，
∴$\frac{1.92}{1.92 + 20 + CA}$=$\frac{1.28}{1.28 + CA}$，
∴CA = 40(米).
∴$\frac{1.28}{AB}$=$\frac{1.28}{1.28 + 40}$，
∴AB = 64.5米.
答:古塔的高度AB为64.5米.