《2025年学考A加同步课时练九年级数学下册人教版》

1. 两角分别__________的两个三角形相似.

答案： 相等.

2. 相似三角形的对应边__________，对应角__________.

答案： 成比例，相等.

1. 下列条件中，一定能判断两个等腰三角形相似的是（ ）
A. 都含有一个40°的内角
B. 都含有一个50°的内角
C. 都含有一个60°的内角
D. 都含有一个70°的内角

答案： C　[解析]因为选项A,B,D给出的角40°,50°,70°可能是顶角也可能是底角，所以不对应，则不能判定两个等腰三角形相似;C、有一个60°的内角的等腰三角形是等边三角形，所有的等边三角形相似，故C正确.故选C.

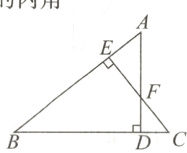
2. 如图，AD⊥BC于点D，CE⊥AB于点E，交AD于点F，则图中相似三角形的对数是（ ）
　　　　　　　　　　　　　　　　　　　　　　　　　　　　
A. 3
B. 4
C. 5
D. 6

答案： D　[解析]
∵AD⊥BC,CE⊥AB,
∴∠AEF=∠ADC=∠BEC=∠ADB=90°.
∵∠AFE=∠CFD,
∴△AFE∽△CFD.
∵∠B是公共角，
∴△ABD∽△CBE.
∵∠A是公共角，
∴△AEF∽△ADB.
∵∠AEF=∠CEB，∠ADC=∠BEC，4个三角形两两相似，共有6对.
∴图中相似三角形的对数是6.故选D.

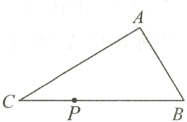
3. 如图，已知点P是Rt△ABC的斜边BC上任意一点，若过点P作直线PD与直角边AB或AC相交于点D，截得的小三角形与△ABC相似，那么D点的位置最多有（ ）
　　　　　　　　　　　　　　　　　　　　　　　　　　　　
A. 2处
B. 3处
C. 4处
D. 5处

答案：
B　[解析]
∵截得的小三角形与△ABC相似，
∴分别过点P作AC的垂线，作AB的垂线，作BC的垂线，所截得的三角形满足题意，则D点的位置最多有3处. 故选B

4. 如图，BE，CD相交于点A，连接BC，DE，下列条件中不能判断△ABC∽△ADE的是（ ）
A. ∠B=∠D
B. ∠C=∠E
C. $\frac{AB}{AC}=\frac{AE}{AD}$
D. $\frac{AB}{AD}=\frac{AC}{AE}$
　　　　 　　

答案： C　[解析]
∵∠BAC=∠DAE,
∴当∠B=∠D或∠C=∠E时,可利用两角对应相等的两个三角形相似证得△ABC∽△ADE,故A、B选项可判断两三角形相似;当$\frac{AB}{AC}=\frac{AD}{AE}$时，可得$\frac{AB}{AE}=\frac{AC}{AD}$，结合∠BAC=∠DAE，则可证得△ABC∽△AED，而不能得出△ABC∽△ADE,故C选项不能判断△ABC ∽△ADE;当$\frac{AB}{AD}=\frac{AC}{AE}$时，结合∠BAC=∠DAE,可证得△ABC∽△ADE,故D选项能判断△ABC ∽△ADE;故选C.

5. 如图，在△ABC中，AB=AC，∠BAC=40°，点D是AC的动点，当∠BDC=__________°时，△ABC∽△BDC.
　　　　

答案： 70　[解析]
∵AB=AC,∠BAC=40°,
∴∠ABC =∠C=70°,
∴∠BDC=70°时,∠C=∠C,∠BDC=∠ABC,
∴△ABC∽△BDC.

6. 如图，△ADE和△ABC中，∠1=∠2，请添加一个适当的条件______________，使△ADE∽△ABC.（只填一个即可）
　　　　

答案： ∠D=∠B或∠E=∠C或$\frac{AD}{AB}=\frac{AE}{AC}$
[解析]
∵∠1=∠2,
∴∠DAE=∠BAC,要使△ADE∽△ABC，则添加的一个条件可以是∠D=∠B或∠E=∠C或$\frac{AD}{AB}=\frac{AE}{AC}$.故答案为∠D=∠B或∠E=∠C或$\frac{AD}{AB}=\frac{AE}{AC}$.