2025年学考A加同步课时练九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 三边__________的两个三角形相似.
答案:
成比例
2. 两边__________且夹角__________的两个三角形相似.
答案:
成比例,相等
1. 下列正方形网格图中的四个三角形中,与甲图中的三角形相似的是( )


答案:
B[解析]设小正方形的边长为1,那么已知三角形的三边长分别为$\sqrt{2},2\sqrt{2},\sqrt{10}$,所以三边之比为$1:2:\sqrt{5}$;
A.三角形的三边长分别为$2,\sqrt{10},3\sqrt{2}$,三边之比为$\sqrt{2}:\sqrt{5}:3$,故本选项错误;
B.三角形的三边长分别为$2,4,2\sqrt{5}$,三边之比为$1:2:\sqrt{5}$,故本选项正确;
C.三角形的三边长分别为$2,3,\sqrt{13}$,三边之比为$2:3:\sqrt{13}$,故本选项错误;
D.三角形的三边长分别为$\sqrt{5},\sqrt{13},4$,三边之比为$\sqrt{5}:\sqrt{13}:4$,故本选项错误.
故选B.
A.三角形的三边长分别为$2,\sqrt{10},3\sqrt{2}$,三边之比为$\sqrt{2}:\sqrt{5}:3$,故本选项错误;
B.三角形的三边长分别为$2,4,2\sqrt{5}$,三边之比为$1:2:\sqrt{5}$,故本选项正确;
C.三角形的三边长分别为$2,3,\sqrt{13}$,三边之比为$2:3:\sqrt{13}$,故本选项错误;
D.三角形的三边长分别为$\sqrt{5},\sqrt{13},4$,三边之比为$\sqrt{5}:\sqrt{13}:4$,故本选项错误.
故选B.
2. 已知△ABC的三边长分别为7.5,9和10.5,△DEF的一边长为5,当△DEF的另两边长是下列哪一组时,这两个三角形相似( )
A. 4,5
B. 5,6
C. 6,7
D. 7,8
A. 4,5
B. 5,6
C. 6,7
D. 7,8
答案:
C[解析]△ABC的三边长分别为7.5,9和10.5,三边的比为$7.5:9:10.5 = 5:6:7$,而△DEF的一边长为5,所以当△DEF的另两边长分别为6,7时,这两个三角形相似.
故选C.
故选C.
3. 如图,在正三角形ABC中,点D,E分别在AC,AB上,且$\frac{AD}{AC}=\frac{1}{3}$,AE = BE,则有( )
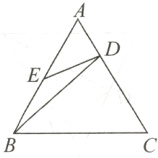
A. △AED∽△ABC
B. △ADB∽△BED
C. △BCD∽△ABC
D. △AED∽△CBD

A. △AED∽△ABC
B. △ADB∽△BED
C. △BCD∽△ABC
D. △AED∽△CBD
答案:
D[解析]
∵△ABC是等边三角形,
∴AB = BC = AC,∠A = ∠C.
∵$\frac{AD}{AC}=\frac{1}{3}$,设AD = x,AC = 3x,则BC = 3x,
CD = 2x,AE = BE = $\frac{3}{2}$x,
∴$\frac{AD}{CD}=\frac{1}{2},\frac{AE}{BC}=\frac{1}{2}$,
∴$\frac{AD}{CD}=\frac{AE}{BC}$,
∴△AED∽△CBD.
故选D.
∵△ABC是等边三角形,
∴AB = BC = AC,∠A = ∠C.
∵$\frac{AD}{AC}=\frac{1}{3}$,设AD = x,AC = 3x,则BC = 3x,
CD = 2x,AE = BE = $\frac{3}{2}$x,
∴$\frac{AD}{CD}=\frac{1}{2},\frac{AE}{BC}=\frac{1}{2}$,
∴$\frac{AD}{CD}=\frac{AE}{BC}$,
∴△AED∽△CBD.
故选D.
4. 在三角形纸片ABC中,AB = 8,BC = 4,AC = 6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )


答案:
D[解析]三角形纸片ABC中,AB = 8,BC = 4,AC = 6.
A.$\frac{4}{AB}=\frac{4}{8}=\frac{1}{2}$,对应边$\frac{AC}{AB}=\frac{6}{8}=\frac{3}{4}\neq\frac{1}{2}$,则沿虚线剪下的阴影部分的三角形与△ABC不相似,故此选项错误;
B.$\frac{3}{AB}=\frac{3}{8}$,对应边$\frac{AC}{AB}=\frac{6}{8}=\frac{3}{4}\neq\frac{3}{8}$,则沿虚线剪下的阴影部分的三角形与△ABC不相似,故此选项错误;
C.$\frac{2}{AC}=\frac{2}{6}=\frac{1}{3}$,对应边$\frac{AC}{AB}=\frac{6}{8}=\frac{3}{4}\neq\frac{1}{3}$,则沿虚线剪下的阴影部分的三角形与△ABC不相似,故此选项错误;
D.$\frac{2}{BC}=\frac{2}{4}=\frac{1}{2}$,对应边$\frac{BC}{AB}=\frac{4}{8}=\frac{1}{2}$,则沿虚线剪下的阴影部分的三角形与△ABC相似,故此选项正确.
故选D.
A.$\frac{4}{AB}=\frac{4}{8}=\frac{1}{2}$,对应边$\frac{AC}{AB}=\frac{6}{8}=\frac{3}{4}\neq\frac{1}{2}$,则沿虚线剪下的阴影部分的三角形与△ABC不相似,故此选项错误;
B.$\frac{3}{AB}=\frac{3}{8}$,对应边$\frac{AC}{AB}=\frac{6}{8}=\frac{3}{4}\neq\frac{3}{8}$,则沿虚线剪下的阴影部分的三角形与△ABC不相似,故此选项错误;
C.$\frac{2}{AC}=\frac{2}{6}=\frac{1}{3}$,对应边$\frac{AC}{AB}=\frac{6}{8}=\frac{3}{4}\neq\frac{1}{3}$,则沿虚线剪下的阴影部分的三角形与△ABC不相似,故此选项错误;
D.$\frac{2}{BC}=\frac{2}{4}=\frac{1}{2}$,对应边$\frac{BC}{AB}=\frac{4}{8}=\frac{1}{2}$,则沿虚线剪下的阴影部分的三角形与△ABC相似,故此选项正确.
故选D.
5. 在△ABC和△DEF中,$\frac{AB}{DE}=\frac{BC}{EF}$. 要使△ABC∽△DEF,还需要添加一个条件,那么这个条件可以是____________________(只需填写一个正确的答案).
答案:
∠B = ∠E(答案不唯一)[解析]在△ABC和△DEF中,$\frac{AB}{DE}=\frac{BC}{EF}$,要使△ABC∽△DEF,需要添加的条件可以是∠B = ∠E(答案不唯一),故答案为∠B = ∠E.
6. 如图,在Rt△OAD中,∠A = 90°,B,C在AD边上,且OA = AB = BC = CD,有下列结论:①△AOB∽△BOD;②△BOC∽△BDO;③△COD∽△BDO,其中成立的有____________________(填序号).


答案:
②[解析]设OA = AB = BC = CD = 1,
∵∠A = 90°,OA = AB = BC = CD,
∴OB = $\sqrt{2}$,OC = $\sqrt{5}$,OD = $\sqrt{10}$,
∴$\frac{OC}{OD}=\frac{\sqrt{2}}{2},\frac{OB}{BD}=\frac{\sqrt{2}}{2}$,
∴$\frac{OC}{OD}=\frac{OB}{BD}$.
∵∠OBD = ∠DBO,
∴△BOC∽△BDO.
故答案为②.
∵∠A = 90°,OA = AB = BC = CD,
∴OB = $\sqrt{2}$,OC = $\sqrt{5}$,OD = $\sqrt{10}$,
∴$\frac{OC}{OD}=\frac{\sqrt{2}}{2},\frac{OB}{BD}=\frac{\sqrt{2}}{2}$,
∴$\frac{OC}{OD}=\frac{OB}{BD}$.
∵∠OBD = ∠DBO,
∴△BOC∽△BDO.
故答案为②.
查看更多完整答案,请扫码查看


