2025年学考A加同步课时练九年级数学下册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年学考A加同步课时练九年级数学下册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 利用反比例函数解决跨学科问题,考查的重点都是对____________的掌握.
答案:
反比例函数.
2. 求解这类问题一是要表示出________,二是要注意自变量的________.
答案:
函数解析式,取值范围.
1. 在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强如下表,则可以反映y与x之间的关系的式子是( )
|体积x(mL)|100|80|60|40|20|
|----|----|----|----|----|----|
|压强y(kPa)|60|75|100|150|300|
A. y = 3000x
B. y = 6000x
C. y = $\frac{3000}{x}$
D. y = $\frac{6000}{x}$
|体积x(mL)|100|80|60|40|20|
|----|----|----|----|----|----|
|压强y(kPa)|60|75|100|150|300|
A. y = 3000x
B. y = 6000x
C. y = $\frac{3000}{x}$
D. y = $\frac{6000}{x}$
答案:
D [解析]由表格数据可得此函数是反比例函数,设解析式为$y = \frac{k}{x}$,则$k = xy = 6000$,故y与x之间的函数解析式是$y = \frac{6000}{x}$,故选D.
2. 公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂 = 动力×动力臂. 小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200 N和0.5 m,则动力F(单位:N)关于动力臂l(单位:m)的函数解析式正确的是( )
A. F = $\frac{1200}{l}$
B. F = $\frac{600}{l}$
C. F = $\frac{500}{l}$
D. F = $\frac{0.5}{l}$
A. F = $\frac{1200}{l}$
B. F = $\frac{600}{l}$
C. F = $\frac{500}{l}$
D. F = $\frac{0.5}{l}$
答案:
B [解析]
∵阻力×阻力臂 = 动力×动力臂,小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200 N和0.5 m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为1200×0.5 = Fl,则$F = \frac{600}{l}$.故选B.
∵阻力×阻力臂 = 动力×动力臂,小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200 N和0.5 m,
∴动力F(单位:N)关于动力臂l(单位:m)的函数解析式为1200×0.5 = Fl,则$F = \frac{600}{l}$.故选B.
3. 已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,则这个反比例函数的解析式为( )

A. I = $\frac{24}{R}$
B. I = $\frac{36}{R}$
C. I = $\frac{48}{R}$
D. I = $\frac{64}{R}$

A. I = $\frac{24}{R}$
B. I = $\frac{36}{R}$
C. I = $\frac{48}{R}$
D. I = $\frac{64}{R}$
答案:
C [解析]设$I = \frac{k}{R}$,把R = 8,I = 6代入得k = 8×6 = 48,故这个反比例函数的解析式为$I = \frac{48}{R}$.故选C.
4. 已知某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P(kPa)是气体体积V(m³)的反比例函数,其图象如图所示,当气球内的气压大于120 kPa时,气球将爆炸. 安全起见,气球的体积应( )

A. 不小于$\frac{4}{5}$ m³
B. 小于$\frac{5}{4}$ m³
C. 不小于$\frac{5}{4}$ m³
D. 小于$\frac{4}{5}$ m³

A. 不小于$\frac{4}{5}$ m³
B. 小于$\frac{5}{4}$ m³
C. 不小于$\frac{5}{4}$ m³
D. 小于$\frac{4}{5}$ m³
答案:
A [解析]设气球内气体的气压P(kPa)和气体体积V(m³)的关系式为$P = \frac{k}{V}$,由图象过点(1.6,60),得k = 96.即$P = \frac{96}{V}$,图象在第一象限内,P随V的增大而减小,
∴当P≤120时,$V\geqslant\frac{96}{120}=\frac{4}{5}$.故选A.
∴当P≤120时,$V\geqslant\frac{96}{120}=\frac{4}{5}$.故选A.
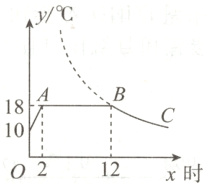
5. 在大棚中栽培新品种的蘑菇,在18℃的条件下生长最快,因此用装有恒温系统的大棚栽培,如图是某天恒温系统从开启升温到保持恒温及关闭过程中大棚内温度y(℃)随时间x(时)变化的函数图象,其中BC段是函数y = $\frac{k}{x}$(k > 0)图象的一部分. 若该蘑菇适宜生长的温度不低于12℃,则这天该种蘑菇适宜生长的时间为( )
A. 18小时
B. 17.5小时
C. 12小时
D. 10小时

A. 18小时
B. 17.5小时
C. 12小时
D. 10小时
答案:
B [解析]把B(12,18)代入$y = \frac{k}{x}$中得k = 12×18 = 216;设一次函数的解析式为y = mx + n,把(0,10),(2,18)代入y = mx + n中,得$\begin{cases}n = 10\\2m + n = 18\end{cases}$,解得$\begin{cases}m = 4\\n = 10\end{cases}$.
∴一次函数的解析式为y = 4x + 10.当y = 12时,12 = 4x + 10,解得x = 0.5;$12=\frac{216}{x}$,解得$x=\frac{216}{12}=18$,
∴18 - 0.5 = 17.5(小时),故选B.
∴一次函数的解析式为y = 4x + 10.当y = 12时,12 = 4x + 10,解得x = 0.5;$12=\frac{216}{x}$,解得$x=\frac{216}{12}=18$,
∴18 - 0.5 = 17.5(小时),故选B.
查看更多完整答案,请扫码查看


