第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
2. △ABO 三个顶点的坐标分别为 A(2,4),B(6,0),C(0,0),以原点 O 为位似中心,把这个三角形缩小为原来的$\frac{1}{2}$,可以得到△A'B'O,则点 A'的坐标是( )
A. (1,2)
B. (1,2)或( - 1, - 2)
C. (2,1)或( - 2, - 1)
D. ( - 2, - 1)
A. (1,2)
B. (1,2)或( - 1, - 2)
C. (2,1)或( - 2, - 1)
D. ( - 2, - 1)
答案:
B
例3 如图,在平面直角坐标系中,△ABC 位于第二象限,点 A 的坐标是( - 2,3),先将△ABC 绕点( - 1,0)顺时针旋转 90°得到△A₁B₁C₁,再以原点 O 为位似中心作△A₁B₁C₁的位似图形△A₂B₂C₂,若△A₁B₁C₁与△A₂B₂C₂的相似比为 1 : 2,则点 A 的对应点 A₂的坐标是( )
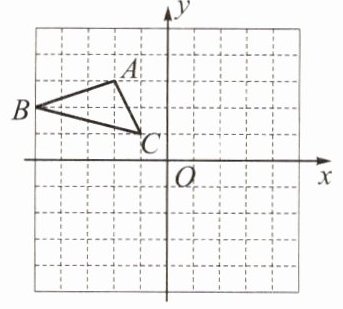
A. (4,2)
B. (6,4)
C. (6,4)或( - 6, - 4)
D. (4,2)或( - 4, - 2)

A. (4,2)
B. (6,4)
C. (6,4)或( - 6, - 4)
D. (4,2)或( - 4, - 2)
答案:
D
例4 如图,A 是反比例函数 y = $\frac{k}{x}$(k≠0)的图象上一点,点 B,D 在 y 轴正半轴上,△ABD 是△COD 关于点 D 的位似图形,且△ABD 与△COD 的相似比为 1 : 3,△ABD 的面积为 1,试求该反比例函数的解析式.
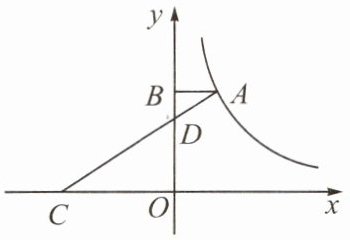
分析:根据△ABD 是△COD 关于点 D 的位似图形,且△ABD 与△COD 的相似比是 1 : 3,可得$\frac{DO}{BD}$ = $\frac{3}{1}$. 设 BD = m,AB = n,则 OB = 4m,根据△ABD 的面积为 1,求出 mn = 2,继而可得出答案.

分析:根据△ABD 是△COD 关于点 D 的位似图形,且△ABD 与△COD 的相似比是 1 : 3,可得$\frac{DO}{BD}$ = $\frac{3}{1}$. 设 BD = m,AB = n,则 OB = 4m,根据△ABD 的面积为 1,求出 mn = 2,继而可得出答案.
答案:
如图,过A作AE⊥x轴于E.
∵△ABD是△COD关于点D的位似图形,且△ABD与△COD的相似比是1∶3,
∴AB/CO = BD/OD = 1/3.
∵四边形ABOE为矩形,
∴AE = OB. 设BD = m,AB = n,则DO = 3m,AE = OB = 4m,CO = 3n.
∵△ABD的面积为1,
∴1/2mn = 1,
∴mn = 2,
∴k = AB·AE = 4mn = 8.
∴该反比例函数的解析式为y = 8/x.
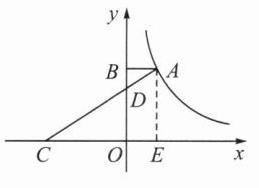
如图,过A作AE⊥x轴于E.
∵△ABD是△COD关于点D的位似图形,且△ABD与△COD的相似比是1∶3,
∴AB/CO = BD/OD = 1/3.
∵四边形ABOE为矩形,
∴AE = OB. 设BD = m,AB = n,则DO = 3m,AE = OB = 4m,CO = 3n.
∵△ABD的面积为1,
∴1/2mn = 1,
∴mn = 2,
∴k = AB·AE = 4mn = 8.
∴该反比例函数的解析式为y = 8/x.

查看更多完整答案,请扫码查看


