《2025年新课程实践与探究丛书九年级数学下册人教版》

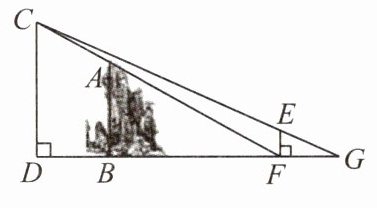
例2 实践课上，亮亮准备用所学知识测量教学楼前一座假山AB的高度. 如图，亮亮在地面上的点F处，眼睛贴地观察，看到假山顶端A、教学楼顶端C在一条直线上. 此时他起身在点F处站直，发现自己的影子末端和教学楼的影子末端恰好重合于点G处，测得FG = 2 m，亮亮的身高EF为1.6 m. 假山的底部B处因有花园围栏，无法到达，但经询问和进行部分测量后得知，BF = 9 m，点D，B，F，G在一条直线上，CD⊥DG，AB⊥DG，EF⊥DG，已知教学楼CD的高度为16 m，请你求出假山的高度AB.

答案： 因为 $CD\perp DG$，$EF\perp DG$，所以 $EF// CD$， 所以 $\triangle GEF\sim\triangle GCD$，所以 $\frac{EF}{CD}=\frac{GF}{GD}$， 即 $\frac{1.6}{16}=\frac{2}{DB + 9+2}$，解得 $BD = 9$. 因为 $CD\perp DG$，$AB\perp DG$，所以 $AB// CD$， 所以 $\triangle FAB\sim\triangle FCD$，所以 $\frac{AB}{CD}=\frac{FB}{FD}$，即 $\frac{AB}{16}=\frac{9}{9 + 9}$， 解得 $AB = 8$，所以假山的高度 $AB$为 $8\ m$.

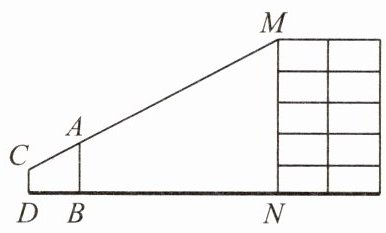
1. 在上完相似三角形一课后，小方设计了一个实验来测量学校教学楼的高度. 如图，在距离教学楼MN为18 m的点B处竖立一个长度为2.8 m的直杆AB，小方调整自己的位置，使得他直立时眼睛所在位置点C，直杆顶点A和教学楼顶点M三点共线. 已知人与直杆的距离DB为2 m，人眼高度CD为1.6 m，则教学楼的高度MN为( )


A. 12 m
B. 12.4 m
C. 13.6 m
D. 15.2 m

答案： C