《2025年新课程实践与探究丛书九年级数学下册人教版》

3. 如图,△ABC∽△ADE,$S_{\triangle ABC}:S_{四边形BDEC}$ = 1 : 3,BC = $\sqrt{2}$,则DE的长为( )


A. $\sqrt{6}$
B. 2$\sqrt{2}$
C. 3$\sqrt{2}$
D. 4$\sqrt{2}$

答案： B

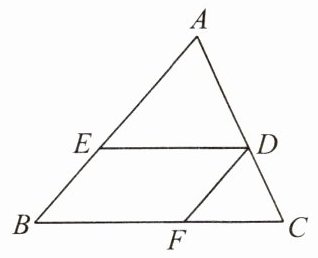
4. 如图,在△ABC中,点D在边AC上,DE//BC,DF//AB.
(1)求证:△DFC∽△AED;
(2)若CD = $\frac{1}{3}$AC,求$\frac{S_{\triangle DFC}}{S_{\triangle AED}}$的值.

答案： （1）因为$DF// AB$，$DE// BC$， 所以$\angle DFC=\angle ABF$，$\angle AED=\angle ABF$，所以$\angle DFC=\angle AED$， 因为$DE// BC$，所以$\angle DCF=\angle ADE$，所以$\triangle DFC\sim\triangle AED$； （2）因为$CD=\frac{1}{3}AC$，所以$\frac{CD}{DA}=\frac{1}{2}$， 由（1）知$\triangle DFC$和$\triangle AED$的相似比为：$\frac{CD}{DA}=\frac{1}{2}$， 所以$\frac{S_{\triangle DFC}}{S_{\triangle AED}}=(\frac{CD}{DA})^2 = (\frac{1}{2})^2=\frac{1}{4}$。

例1 小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高. 如图所示，在某一时刻，他们在阳光下分别测得该建筑物OB的影长OC为16 m，OA的影长OD为20 m，小明的影长FG为2.4 m，其中O，C，D，F，G五点在同一直线上，A，B，O三点在同一直线上，且AO⊥OD，EF⊥FG. 已知小明的身高EF为1.8 m，求旗杆的高AB.

答案： $AB = 3\ m$.