第29页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
例1 如图,已知△ABE∽△CDE,AD,BC相交于点E, △ABE与△CDE的周长之比是$\frac{2}{5}$,若AE = 2,BE = 1,则BC的长为( )
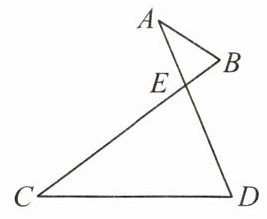
A. 3
B. 4
C. 5
D. 6

A. 3
B. 4
C. 5
D. 6
答案:
D
例2 图①是伸缩折叠不锈钢晾衣架的实物图,图②是它的侧面示意图,AD与CB相交于点O,AB//CD,根据图②中的数据可得x的值为( )
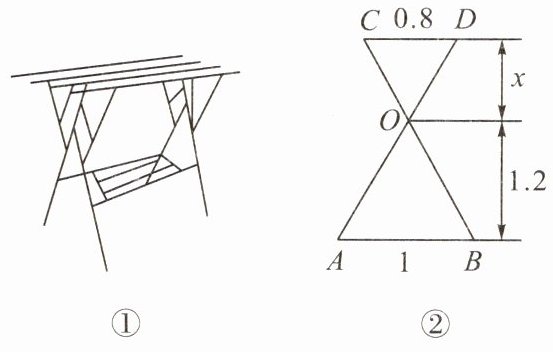
A. 0.8
B. 0.96
C. 1
D. 1.08

A. 0.8
B. 0.96
C. 1
D. 1.08
答案:
B
1. △ABC的三边长分别为2,3,4,另有一个与它相似的三角形DEF,其最长边为12,则△DEF的周长是( )
A. 54
B. 36
C. 27
D. 21
A. 54
B. 36
C. 27
D. 21
答案:
C
2. 如图,Rt△ABC∽Rt△DFE,CM,EN分别是斜边AB,DF上的中线,已知AC = 9,CB = 12,DE = 3.
(1)求CM和EN的长.
(2)$\frac{CM}{EN}$的值与相似比有什么关系? 你能得到什么结论?
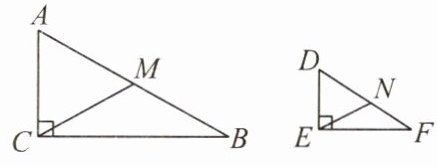
(1)求CM和EN的长.
(2)$\frac{CM}{EN}$的值与相似比有什么关系? 你能得到什么结论?

答案:
(1)$CM = 7.5$,$EN = 2.5$。
(2)因为$\frac{CM}{EN}=\frac{7.5}{2.5}=\frac{3}{1}$,相似比为$\frac{AC}{DE}=\frac{9}{3}=\frac{3}{1}$,
所以相似三角形对应中线的比等于相似比。
查看更多完整答案,请扫码查看


