《2025年新课程实践与探究丛书九年级数学下册人教版》

例2 已知线段a,b,c，如果a : b : c = 1 : 2 : 3，那么$\frac{a + 3b}{2c + b}$ : $\frac{a + b}{c + b}$的值是( )
A. $\frac{7}{6}$ : $\frac{1}{3}$
B. $\frac{6}{7}$ : $\frac{2}{3}$
C. $\frac{7}{8}$ : $\frac{3}{5}$
D. $\frac{8}{7}$ : $\frac{5}{3}$

答案： C

1. 四条线段a,b,c,d成比例，其中a = 2 cm,b = 3 cm,d = 6 cm，则线段c的长为( )
A. 1 cm
B. 4 cm
C. 9 cm
D. 12 cm

答案： B

2. 如果在比例尺为1 : 2 000 000的地图上，A,B两地的图上距离是3.4 cm，那么A,B两地的实际距离是_______km.

答案： 68

例3 如图，四边形ABCD和四边形EFGH相似，且顶点都在方格纸的格点上，它们的相似比是( )


A. 1 : 2
B. 1 : 4
C. 2 : 1
D. 4 : 1

答案： C

例4 如图，在矩形ABCD中，AB = 4，点E,F分别在边AD,BC上，且EF⊥BC. 若矩形ABFE∽矩形DEFC，且相似比为1 : 2，求AD的长.

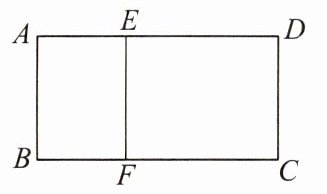
分析：利用相似多边形的性质得到$\frac{AB}{DE}$ = $\frac{AE}{DC}$ = $\frac{1}{2}$，而根据矩形的性质得到CD = AB = 4，从而利用比例性质得到DE = 8，AE = 2，然后计算AE + DE即可.

答案：
∵矩形ABFE∽矩形DEFC，且相似比为1∶2，
∴$\frac{AB}{DE}=\frac{AE}{DC}=\frac{1}{2}$。
∵四边形ABCD为矩形，
∴CD = AB = 4，
∴$\frac{4}{DE}=\frac{AE}{4}=\frac{1}{2}$，
∴DE = 8，AE = 2，
∴AD = AE + DE = 2 + 8 = 10。