《2025年新课程实践与探究丛书九年级数学下册人教版》

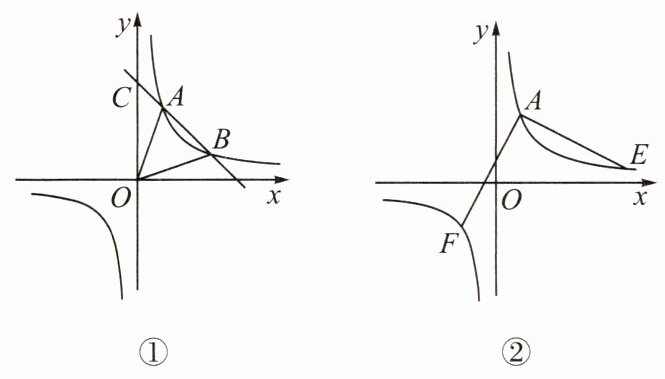
3. 如图①，反比例函数$y = \frac{m}{x}(m \neq 0)$与一次函数$y = kx + b(k \neq 0)$的图象交于点$A(1,3)$，点$B(n,1)$，一次函数$y = kx + b(k \neq 0)$与$y$轴相交于点$C$.
(1)求反比例函数和一次函数的解析式；
(2)连接$OA$，$OB$，求$\triangle OAB$的面积；
(3)如图②，$E$是反比例函数图象上点$A$右侧一点，连接$AE$，把线段$AE$绕点$A$顺时针旋转$90^{\circ}$，点$E$的对应点$F$恰好也落在这个反比例函数的图象上，求点$E$的坐标.

答案：

(1) 反比例函数的解析式为 $y = \frac{3}{x}$，一次函数的解析式 $y = -x + 4$。
(2) $S_{\triangle AOB}=S_{\triangle BOC}-S_{\triangle AOC}=\frac{1}{2}\times4\times(3 - 1)=4$。
(3) 如图，过点 $A$ 作 $x$ 轴的平行线 $CD$，作 $FC\perp CD$ 于 $C$，$ED\perp CD$ 于 $D$，设 $E(a,\frac{3}{a})(a ＞ 1)$，$\because A(1,3)$，$\therefore AD = a - 1$，$DE = 3-\frac{3}{a}$，$\because$ 把线段 $AE$ 绕点 $A$ 顺时针旋转 $90^{\circ}$，点 $E$ 的对应点 $F$ 恰好也落在这个反比例函数的图象上，$\therefore\angle EAF = 90^{\circ}$，$AE = AF$，$\therefore\angle EAD+\angle CAF = 90^{\circ}$，$\because\angle EAD+\angle AED = 90^{\circ}$，$\therefore\angle CAF=\angle AED$，在 $\triangle ACF$ 和 $\triangle EDA$ 中，$\begin{cases}\angle CAF=\angle AED \\\angle ACF=\angle EDA = 90^{\circ} \\AF = EA\end{cases}$$\therefore\triangle ACF\cong\triangle EDA(AAS)$，$\therefore CF = AD = a - 1$，$AC = DE = 3-\frac{3}{a}$，$\therefore F(\frac{3}{a}-2,4 - a)$，$\because F$ 恰好也落在这个反比例函数的图象上，$\therefore(\frac{3}{a}-2)(4 - a)=3$，解得 $a = 6$ 或 $a = 1$（舍去），$\therefore E(6,\frac{1}{2})$。