4. 一个圆锥与一个圆柱的高相等,体积之比是2∶5,已知圆柱的底面积是15 cm²,则圆锥的底面积是( )cm²。
A. 6
B. 9
C. 12
D. 18
A. 6
B. 9
C. 12
D. 18
答案:
D
1. 求下面图形的体积。
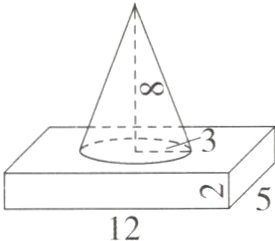

答案:
$12×2×5+\frac{1}{3}×3.14×3^{2}×8 = 195.36(cm^{3})$
2. 求下面图形的表面积。
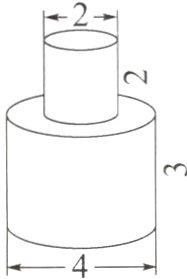

答案:
$3.14×(4÷2)^{2}×2 + 3.14×4×3 + 3.14×2×2 = 75.36(cm^{2})$
1. 一个装有水的圆柱形容器的底面积是31.4 cm²,水中浸没着一个底面半径为3 cm、高为10 cm的圆锥形石块。当取出石块后,容器中的水面会下降多少厘米?
答案:
圆锥形石块的体积:$\frac{1}{3}×3.14×3^{2}×10 = 94.2(cm^{3})$
$94.2÷31.4 = 3(cm)$
$94.2÷31.4 = 3(cm)$
2. 有一种铁质零件(如图),外形是圆柱,底面直径是4 cm,高是5 cm,零件正中间打穿一个边长为2 cm的正方形孔。
(1)这个零件的体积是多少立方厘米?

(2)为防止生锈,零件与空气接触部分都要喷上漆,需喷漆的面积有多少平方厘米? (得数保留整数)
(1)这个零件的体积是多少立方厘米?

(2)为防止生锈,零件与空气接触部分都要喷上漆,需喷漆的面积有多少平方厘米? (得数保留整数)
答案:
(1) $3.14×(4÷2)^{2}×5 - 2×2×5 = 42.8(cm^{3})$
(2) 侧面积:$3.14×4×5 = 62.8(cm^{2})$
底面积:$3.14×(4÷2)^{2}×2 - 2×2×2 = 17.12(cm^{2})$
长方体侧面积:$2×5×4 = 40(cm^{2})$
$62.8 + 17.12 + 40≈120(cm^{2})$
(1) $3.14×(4÷2)^{2}×5 - 2×2×5 = 42.8(cm^{3})$
(2) 侧面积:$3.14×4×5 = 62.8(cm^{2})$
底面积:$3.14×(4÷2)^{2}×2 - 2×2×2 = 17.12(cm^{2})$
长方体侧面积:$2×5×4 = 40(cm^{2})$
$62.8 + 17.12 + 40≈120(cm^{2})$
3. 《九章算术》中有如下问题:“今有委米依垣内角,下周八尺,高五尺。问积及为米几何?”其意思为“在屋内墙角处堆放米(如图,米堆为一个圆锥的$\frac{1}{4}$),米堆底部的弧长为8尺,米堆的高为5尺。问米堆的体积及堆放的米各为多少?”已知一斛米的体积约为1.62立方尺,π取3。则堆放的米约为多少斛? 如果将这些米放进底面积为12平方尺的圆柱形容器内,那么米高为几尺? (得数都保留整数)
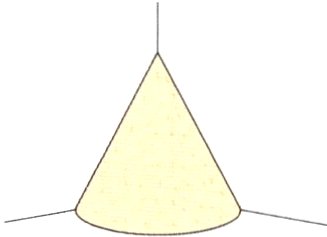

答案:
$\frac{1}{4}×\frac{1}{3}×3×(4×8÷2÷3)^{2}×5≈36$(立方尺)
$36÷1.62≈22$(斛) $36÷12 = 3$(尺)
$36÷1.62≈22$(斛) $36÷12 = 3$(尺)
查看更多完整答案,请扫码查看


