《2025年阳光同学课时优化作业六年级数学下册人教版》

1.
　　
(1)图中圆锥的体积是圆柱(　　　)的体积的$\frac{1}{3}$，与圆锥体积相等的是圆柱(　　　)。
A. ①
B. ②
C. ③
(2)圆柱①的体积是圆柱②的体积的(　　　)倍，是圆柱③的体积的(　　　)倍。
A. 3
B. 4
C. 6
D. 8

答案：
(1)A C
(2)B A

2. 一段长、宽、高的比是5∶4∶3的长方体木材，棱长总和是48 cm，把它加工成一个最大的圆柱，再把圆柱削成一个最大的圆锥，则圆锥的体积是(　　　　)cm³。

答案： 12.56

3. 将一个高是7 cm的圆柱，沿着底面直径和高分成两个半圆柱(如图)，切面的面积一共是70 cm²，这个圆柱的底面周长是(　　　　)cm。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： 15.7

4. 把一根长20 m的圆柱形木料按3∶7的比锯成两段小圆柱后，表面积增加了8 dm²，较长的一段木料的体积是(　　　)dm³。
A. 48
B. 56
C. 560
D. 800

答案： C

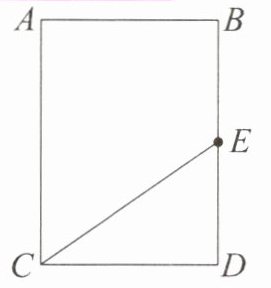
5. 如图，E是BD的中点，将三角形CED以ED边所在的直线为轴旋转一周得到图形甲，将长方形ABDC以BD边所在的直线为轴旋转一周得到图形乙。甲、乙两图形的体积比为(　　　　　　)。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： 1:6

6. 如图，阳阳和光光分别以直角梯形的上底和下底所在的直线为轴，将直角梯形旋转一周，得到了两个立体图形。阳阳说：“我们旋转的平面图形是完全一样的，所以旋转后得到的两个立体图形的体积也相等。”光光说：“我不同意你的看法，我认为两个立体图形的体积不相等。”
(1)我同意(　　　　)的说法。
(2)旋转得到的两个立体图形的体积比是多少？(请写出思考过程)
　　　　　　　　　　　　　　　　　　　　　　　　　　　　

答案：
(1)光光
(2)阳阳：$\pi\times3^{2}\times6 - \pi\times3^{2}\times(6 - 3)\times\frac{1}{3}=45\pi(\text{cm}^{3})$
光光：$\pi\times3^{2}\times3 + \pi\times3^{2}\times(6 - 3)\times\frac{1}{3}=36\pi(\text{cm}^{3})$
$45\pi:36\pi = 5:4$