《2025年聚能闯关期末复习冲刺卷七年级数学下册人教版》

2. (8分)求下列各式中$x$的值.
(1)$4x^{2}-9 = 0$； (2)$(x - 2)^{3}=-0.125$.

答案： 解：（1）$x = \pm\frac{3}{2}$. （2）$x = 1.5$.

3. (6分)已知$|x|=\sqrt{5}$，$y$是3的平方根，且$|y - x| = x - y$，求$x + y$的值.

答案： 解：由题意，得$x = \pm\sqrt{5}$，$y = \pm\sqrt{3}$.
∵$|y - x| = x - y$，
∴$x ＞ y$.
∴$x = \sqrt{5}$，$y = \sqrt{3}$或$x = \sqrt{5}$，$y = - \sqrt{3}$.
∴$x + y = \sqrt{5} + \sqrt{3}$或$x + y = \sqrt{5} - \sqrt{3}$.

4. (6分)若$\sqrt{a + 8}$与$(b - 27)^{2}$互为相反数，求$\sqrt[3]{a}-\sqrt[3]{b}$的立方根.

答案： 解：
∵$\sqrt{a + 8}$与$(b - 27)^2$互为相反数，
∴$\sqrt{a + 8} + (b - 27)^2 = 0$. 而$\sqrt{a + 8} \geq 0$，$(b - 27)^2 \geq 0$，
∴$\sqrt{a + 8} = 0$，$(b - 27)^2 = 0$.
∴$a = - 8$，$b = 27$.
∴$\sqrt[3]{a} - \sqrt[3]{b} = - 2 - 3 = - 5$.
∴$\sqrt[3]{a} - \sqrt[3]{b}$的立方根为$\sqrt[3]{- 5} = - \sqrt[3]{5}$.

5. (8分)如图，实数$a$，$b$，$c$在数轴上的对应点分别为$A$，$B$，$C$，化简$\sqrt{(a + b)^{2}}-|c - b|+|a + c|$.

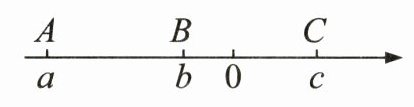
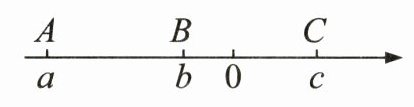
答案： 解：由题图可知$a ＜ b ＜ c$且$|a| ＞ |c|$，$|b| ＜ |c|$，
∴$a + b ＜ 0$，$c - b ＞ 0$，$a + c ＜ 0$.
∴$\sqrt{(a + b)^2} - |c - b| + |a + c|$ = - (a + b) - (c - b) - (a + c) = - a - b - c + b - a - c = - 2a - 2c.