《2025年通城学典课时作业本九年级数学下册华师大版》

一、选择题（每小题 3 分，共 24 分）

答案：

1. 若函数$y = mx(x - 1) - x^{2}$是关于$x$的二次函数，则$m$的取值范围是 （ ）
A. $m \neq 0$
B. $m \neq - 1$
C. $m \neq 1$
D. $m \neq \pm 1$

答案：

2. 已知$A(x_{1},y_{1})$、$B(x_{2},y_{2})$是抛物线$y = \frac{1}{2}x^{2} + 1$上的点，且$|x_{1}| ＜ |x_{2}|$，则$y_{1}$与$y_{2}$的大小关系为（ ）
A. $y_{1} ＜ y_{2}$
B. $y_{1} ＞ y_{2}$
C. $y_{1} = y_{2}$
D. 无法确定

答案：

3. 抛物线$y = - 2(x - 1)^{2} - 1$可由抛物线$y = - 2(x + 2)^{2} + 3$平移得到，那么平移过程是 （ ）
A. 先向右平移 3 个单位，再向下平移 4 个单位
B. 先向右平移 3 个单位，再向上平移 4 个单位
C. 先向左平移 3 个单位，再向下平移 4 个单位
D. 先向左平移 3 个单位，再向上平移 4 个单位

答案：

4. 抛物线$y = ax^{2} + bx + c(a \neq 0)$上部分点的横坐标$x$、纵坐标$y$的对应值如下表：
| $x$ | -2 | -1 | 0 | 1 |
| ---- | ---- | ---- | ---- | ---- |
| $y$ | 0 | 4 | 6 | 6 |
则下列结论中，不正确的是 （ ）
A. 抛物线的开口向下
B. 抛物线的对称轴为直线$x = \frac{1}{2}$
C. 抛物线与$x$轴的一个交点坐标为$(2,0)$
D. 函数$y = ax^{2} + bx + c$的最大值为$\frac{25}{4}$

答案：

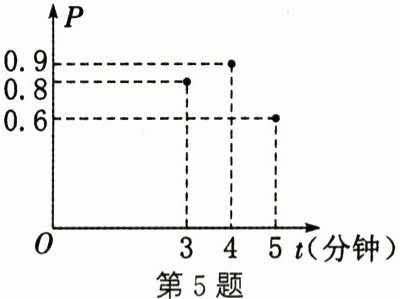
5. 在加工煎炸豆腐时，我们把“焦脆而不煳”的豆腐块数的百分比称为“可食用率”. 在特定条件下，“可食用率”$P$与加工煎炸时间$t$（分钟）近似满足的函数关系为$P = at^{2} + bt + c(a、b、c$是常数，$a \neq 0)$，如图所示为三次加工的数据. 根据上述函数关系和加工数据，可以得到加工煎炸豆腐的最佳时间为 （ ）

A. 3.50 分钟
B. 4.05 分钟
C. 3.75 分钟
D. 4.25 分钟

答案：

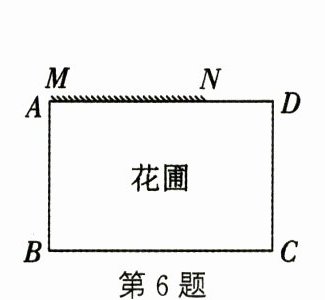
6. 利用一段长为 8 m 的旧直墙$MN$与长为 32 m 的篱笆围成如图所示的矩形花圃，则围成的矩形花圃的最大面积为 （ ）

A. $90\ m^{2}$
B. $96\ m^{2}$
C. $100\ m^{2}$
D. $128\ m^{2}$

答案：

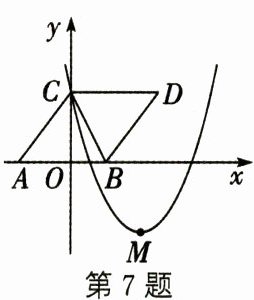
7. 如图，在平面直角坐标系中，菱形$ABDC$的边$AB$在$x$轴上，顶点$C$在$y$轴上，$A( - 3,0)$，$C(0,4)$，抛物线$y = ax^{2} - 8ax + c$经过点$C$，且顶点$M$在直线$BC$上，则$a$的值为 （ ）

A. $\frac{2}{5}$
B. $\frac{1}{2}$
C. $\frac{3}{4}$
D. $\frac{2}{3}$

答案：