2025年金版教程高中新课程创新导学案高中物理选择性必修第二册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年金版教程高中新课程创新导学案高中物理选择性必修第二册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第26页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
实践提升
例2 回旋加速器的工作原理如图1所示,置于真空中的D形金属盒半径为R,两盒间狭缝的间距为d,磁感应强度为B的匀强磁场与盒面垂直,被加速粒子的质量为m,电荷量为+q,加在狭缝间的交变电压如图2所示,电压值的大小为U₀,周期$T = \frac{2\pi m}{qB}$。一束该种粒子在t = 0时刻从A处均匀地飘入狭缝,其初速度视为零。现考虑粒子在狭缝中的运动时间,假设能够出射的粒子每次经过狭缝均做加速运动,不考虑粒子间的相互作用。求:
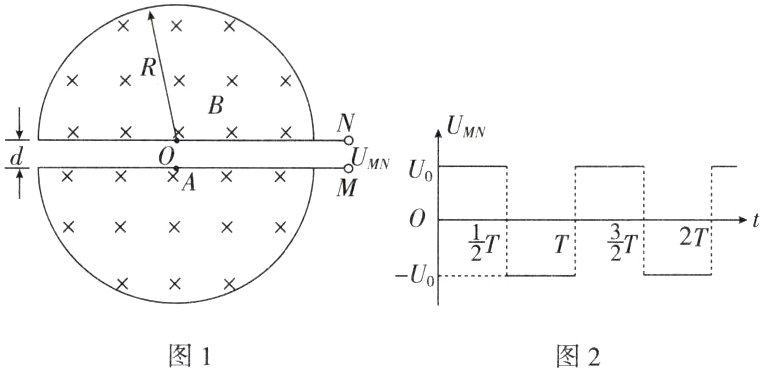
(1)出射粒子的动能E_{km};
(2)粒子从飘入狭缝至动能达到E_{km}所需的总时间t₀。
[实践探究](1)出射粒子的速度由什么决定?______________________________
(2)总时间是被加速的次数直接乘以带电粒子在磁场中运动时周期的一半吗?______________________________
[规范解答]______________________________
例2 回旋加速器的工作原理如图1所示,置于真空中的D形金属盒半径为R,两盒间狭缝的间距为d,磁感应强度为B的匀强磁场与盒面垂直,被加速粒子的质量为m,电荷量为+q,加在狭缝间的交变电压如图2所示,电压值的大小为U₀,周期$T = \frac{2\pi m}{qB}$。一束该种粒子在t = 0时刻从A处均匀地飘入狭缝,其初速度视为零。现考虑粒子在狭缝中的运动时间,假设能够出射的粒子每次经过狭缝均做加速运动,不考虑粒子间的相互作用。求:

(1)出射粒子的动能E_{km};
(2)粒子从飘入狭缝至动能达到E_{km}所需的总时间t₀。
[实践探究](1)出射粒子的速度由什么决定?______________________________
(2)总时间是被加速的次数直接乘以带电粒子在磁场中运动时周期的一半吗?______________________________
[规范解答]______________________________
答案:
[实践探究]
(1)提示:由$r=\frac{mv}{qB}$可知,$v_{m}$由磁感应强度B和D形盒半径R决定。
(2)提示:由于此处考虑粒子在狭缝中的运动时间,总时间应为$t_{0}=(n - 1)\cdot\frac{T}{2}+\Delta t(\Delta t$是经过狭缝被加速的总时间)。
[规范解答]
(1)粒子在磁场中的运动半径为R时,$qv_{m}B = m\frac{v_{m}^{2}}{R}$,且$E_{km}=\frac{1}{2}mv_{m}^{2}$
解得$E_{km}=\frac{q^{2}B^{2}R^{2}}{2m}$。
(2)设粒子被加速n次达到动能$E_{km}$,则$E_{km}=nqU_{0}$
解得$n=\frac{qB^{2}R^{2}}{2mU_{0}}$
粒子在狭缝间的运动可等效成匀加速直线运动,设n次经过狭缝的总时间为$\Delta t$,
粒子经过狭缝时的加速度$a=\frac{qU_{0}}{md}$
根据匀变速直线运动的规律有$nd=\frac{1}{2}a\cdot(\Delta t)^{2}$
解得$\Delta t=\frac{BRd}{U_{0}}$
由$t_{0}=(n - 1)\cdot\frac{T}{2}+\Delta t$
解得$t_{0}=\frac{\pi BR^{2}+2BRd}{2U_{0}}-\frac{\pi m}{qB}$。
[答案]
(1)$\frac{q^{2}B^{2}R^{2}}{2m}$
(2)$\frac{\pi BR^{2}+2BRd}{2U_{0}}-\frac{\pi m}{qB}$
(1)提示:由$r=\frac{mv}{qB}$可知,$v_{m}$由磁感应强度B和D形盒半径R决定。
(2)提示:由于此处考虑粒子在狭缝中的运动时间,总时间应为$t_{0}=(n - 1)\cdot\frac{T}{2}+\Delta t(\Delta t$是经过狭缝被加速的总时间)。
[规范解答]
(1)粒子在磁场中的运动半径为R时,$qv_{m}B = m\frac{v_{m}^{2}}{R}$,且$E_{km}=\frac{1}{2}mv_{m}^{2}$
解得$E_{km}=\frac{q^{2}B^{2}R^{2}}{2m}$。
(2)设粒子被加速n次达到动能$E_{km}$,则$E_{km}=nqU_{0}$
解得$n=\frac{qB^{2}R^{2}}{2mU_{0}}$
粒子在狭缝间的运动可等效成匀加速直线运动,设n次经过狭缝的总时间为$\Delta t$,
粒子经过狭缝时的加速度$a=\frac{qU_{0}}{md}$
根据匀变速直线运动的规律有$nd=\frac{1}{2}a\cdot(\Delta t)^{2}$
解得$\Delta t=\frac{BRd}{U_{0}}$
由$t_{0}=(n - 1)\cdot\frac{T}{2}+\Delta t$
解得$t_{0}=\frac{\pi BR^{2}+2BRd}{2U_{0}}-\frac{\pi m}{qB}$。
[答案]
(1)$\frac{q^{2}B^{2}R^{2}}{2m}$
(2)$\frac{\pi BR^{2}+2BRd}{2U_{0}}-\frac{\pi m}{qB}$
[变式训练2](多选)回旋加速器工作原理示意图如图所示,磁感应强度为B的匀强磁场与盒面垂直,两盒间的狭缝很小,粒子穿过的时间可忽略,它们接在电压为U、频率为f的交流电源上。若A处粒子源产生的质子在加速器中被加速,下列说法正确的是 ( )
A. 若只增大交流电压U,则质子获得的最大动能增大
B. 若只增大交流电压U,则质子达到最大动能所需的加速次数会减少
C. 若磁感应强度B增大,交流电频率f必须适当增大才能正常工作
D. 不改变磁感应强度B和交流电频率f,该回旋加速器也能用于加速α粒子
A. 若只增大交流电压U,则质子获得的最大动能增大
B. 若只增大交流电压U,则质子达到最大动能所需的加速次数会减少
C. 若磁感应强度B增大,交流电频率f必须适当增大才能正常工作
D. 不改变磁感应强度B和交流电频率f,该回旋加速器也能用于加速α粒子
答案:
[变式训练2] BC [设D形盒的半径为R,当粒子从D形盒中出来时速度最大,根据$qv_{m}B = m\frac{v_{m}^{2}}{R}$,得$v_{m}=\frac{qBR}{m}$,那么质子获得的最大动能$E_{km}=\frac{1}{2}mv_{m}^{2}=\frac{q^{2}B^{2}R^{2}}{2m}$,则最大动能与交流电压U无关,故A错误;从开始至达到最大动能,有$nqU = E_{km}$,可得加速次数$n=\frac{E_{km}}{qU}$,则只增大U,加速次数n会减少,故B正确;根据$T=\frac{2\pi m}{Bq}$,若磁感应强度B增大,那么T会减小,加速电场的周期应与带电粒子在磁场中运动的周期相等,故交流电频率f必须适当增大才能正常工作,故C正确;根据$T=\frac{2\pi m}{qB}$知,$\alpha$粒子的比荷与质子的不同,故需改变交流电的频率f或磁感应强度B才能加速$\alpha$粒子,故D错误。]
查看更多完整答案,请扫码查看


