第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
1. 给$2$、$4$、$\frac{5}{8}$这三个数配上第四个数$x$,使得这四个数能组成比例,那么$x$最小是( )。
A. $\frac{5}{16}$
B. $\frac{5}{4}$
C. $\frac{64}{5}$
D. $\frac{5}{18}$
A. $\frac{5}{16}$
B. $\frac{5}{4}$
C. $\frac{64}{5}$
D. $\frac{5}{18}$
答案:
给2、4、$\frac{5}{8}$这三个数配上第四个数$x$,使得这四个数能组成比例,那么$x$最小是(A)。
A. $\frac{5}{16}$ B. $\frac{5}{4}$ C. $\frac{64}{5}$ D. $\frac{5}{18}$
2. 甲数的$\frac{5}{4}$等于乙数的$\frac{3}{2}$(甲、乙两数均不为$0$),那么甲数:乙数=( )。
A. $\frac{3}{2}:\frac{4}{5}$
B. $\frac{5}{4}:\frac{3}{2}$
C. $5:6$
D. $6:5$
A. $\frac{3}{2}:\frac{4}{5}$
B. $\frac{5}{4}:\frac{3}{2}$
C. $5:6$
D. $6:5$
答案:
甲数的$\frac{5}{4}$等于乙数的$\frac{3}{2}$(甲、乙两数均不为0),那么甲数∶乙数=(D)。
A. $\frac{3}{2}:\frac{4}{5}$ B. $\frac{5}{4}:\frac{3}{2}$ C. 5∶6 D. 6∶5
3. 将下图的三角形$ABC$按$3:1$的比放大后,下面选项中有变化的是( )。
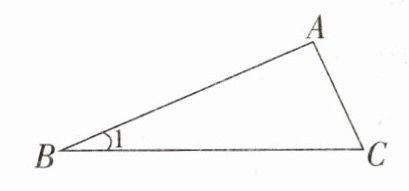
①线段$AC$的长度 ②三角形$ABC$的面积 ③$\angle 1$的度数 ④$AC$的长度与$BC$的长度的比值
A. ①② B. ①②③ C. ③④ D. ①②③④

①线段$AC$的长度 ②三角形$ABC$的面积 ③$\angle 1$的度数 ④$AC$的长度与$BC$的长度的比值
A. ①② B. ①②③ C. ③④ D. ①②③④
答案:
将下图的三角形$ABC$按3∶1的比放大后,下面选项中有变化的是(A)。
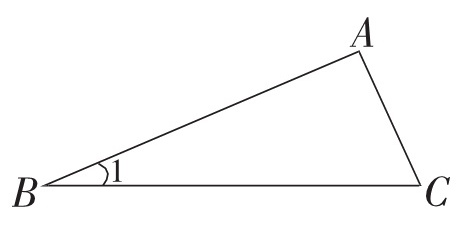
①线段$AC$的长度 ②三角形$ABC$的面积 ③$\angle1$的度数 ④$AC$的长度与$BC$的长度的比值 A. ①② B. ①②③ C. ③④ D. ①②③④
将下图的三角形$ABC$按3∶1的比放大后,下面选项中有变化的是(A)。

①线段$AC$的长度 ②三角形$ABC$的面积 ③$\angle1$的度数 ④$AC$的长度与$BC$的长度的比值 A. ①② B. ①②③ C. ③④ D. ①②③④
4. 在比例$60:35 = 36:21$中,如果将右边的比的前项减去$30$,两个比的后项不变,那么左边的比的前项应减去( ),才能使该比例成立。
A. $60$
B. $50$
C. $40$
D. $30$
A. $60$
B. $50$
C. $40$
D. $30$
答案:
在比例60∶35 = 36∶21中,如果将右边的比的前项减去30,两个比的后项不变,那么左边的比的前项应减去(B),才能使该比例成立。
A. 60 B. 50 C. 40 D. 30
5. 下列式子中,$x$、$y$均不为$0$,则$x$和$y$成反比例关系的是( )。
A. $x\div y = 3.14$
B. $x = 2.1 - y$
C. $x = y + 2024$
D. $xy = 3.14$
A. $x\div y = 3.14$
B. $x = 2.1 - y$
C. $x = y + 2024$
D. $xy = 3.14$
答案:
下列式子中,$x$、$y$均不为0,则$x$和$y$成反比例关系的是(D)。
A. $x\div y = 3.14$ B. $x = 2.1 - y$ C. $x = y + 2024$ D. $xy = 3.14$
6. 按下图的程序操作,输出的数与输入的数( )。
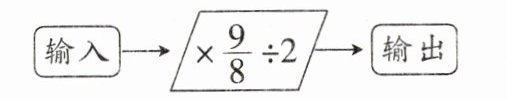
A. 成正比例关系
B. 成反比例关系
C. 不成比例关系
D. 无法确定是否成比例关系
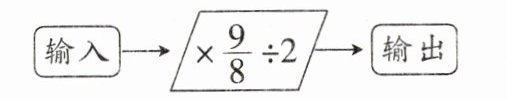
A. 成正比例关系
B. 成反比例关系
C. 不成比例关系
D. 无法确定是否成比例关系
答案:
按下图的程序操作,输出的数与输入的数(A)。

A. 成正比例关系 B. 成反比例关系 C. 不成比例关系 D. 无法确定是否成比例关系
按下图的程序操作,输出的数与输入的数(A)。

A. 成正比例关系 B. 成反比例关系 C. 不成比例关系 D. 无法确定是否成比例关系
7. 学校采购了一批跳绳,按$2:3:4$的比分给六年级$1$班、$2$班、$3$班。已知$1$班比$3$班少分$18$根跳绳,那么$2$班分到了( )根跳绳。
A. $9$
B. $18$
C. $27$
D. $36$
A. $9$
B. $18$
C. $27$
D. $36$
答案:
学校采购了一批跳绳,按2∶3∶4的比分给六年级1班、2班、3班。已知1班比3班少分18根跳绳,那么2班分到了(C)根跳绳。
A. 9 B. 18 C. 27 D. 36
8. 王老师每天从家到学校,如果骑电动车,需要$12$分钟;如果骑自行车,需要$32$分钟。那么王老师骑电动车的速度和骑自行车的速度的最简单的整数比是( )。
A. $12:32$
B. $32:12$
C. $3:8$
D. $8:3$
A. $12:32$
B. $32:12$
C. $3:8$
D. $8:3$
答案:
王老师每天从家到学校,如果骑电动车,需要12分钟;如果骑自行车,需要32分钟。那么王老师骑电动车的速度和骑自行车的速度的最简单的整数比是(D)。
A. 12∶32 B. 32∶12 C. 3∶8 D. 8∶3
9. 一个真分数,如果分子、分母同时加$59$,约分后等于$\frac{1}{2}$;如果分子、分母同时加$23$,约分后等于$\frac{1}{3}$。那么分子、分母同时加( ),约分后等于$\frac{1}{4}$。
A. $9$
B. $11$
C. $13$
D. $15$
A. $9$
B. $11$
C. $13$
D. $15$
答案:
一个真分数,如果分子、分母同时加59,约分后等于$\frac{1}{2}$;如果分子、分母同时加23,约分后等于$\frac{1}{3}$。那么分子、分母同时加(B),约分后等于$\frac{1}{4}$。
A. 9 B. 11 C. 13 D. 15
查看更多完整答案,请扫码查看


