《2025年作业本江西教育出版社六年级数学下册人教版》

18. 数学活动课上，老师准备了一个装满水的圆锥形容器和4个空的容器(如下图所示)，并向同学们提出了一个问题：将圆锥形容器中的这些水分别倒入A、B、C、D四个容器中，倒入哪个容器中，恰好能装满? 请你写出思考的过程和结论。(单位：cm，以下数据都是从容器内部测量的)

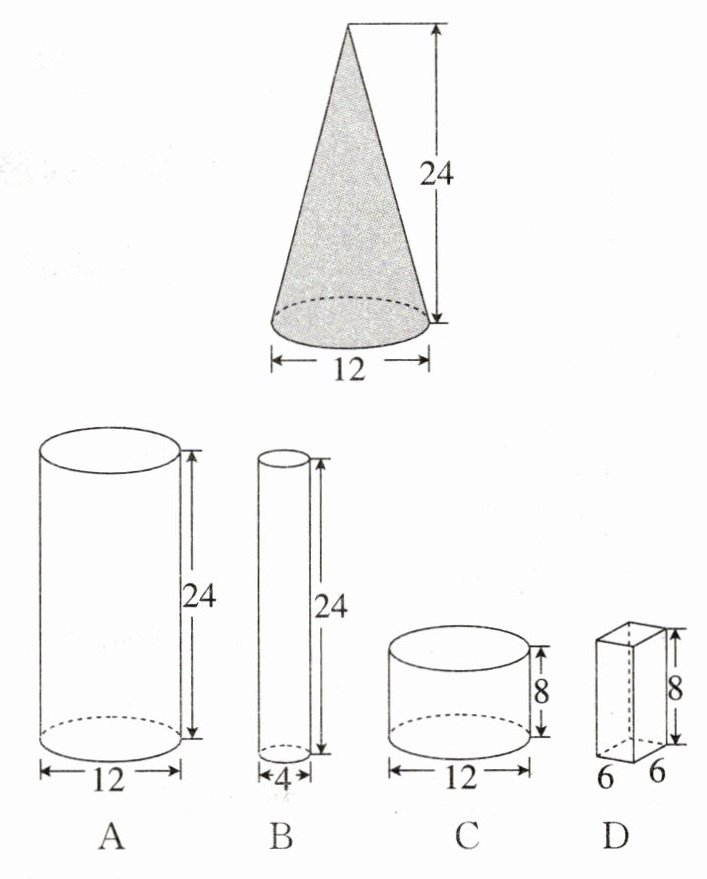
(1)思考过程：
(2)结论：

答案： （1）思考过程： 方法一：圆锥与圆柱A比较，等底等高的圆柱和圆锥，圆锥的容积是圆柱容积的$\frac{1}{3}$；圆锥与圆柱B比较，圆锥的半径是圆柱半径的3倍，圆锥的容积是圆柱容积的3倍；圆锥与圆柱C比较，等底的圆柱和圆锥，圆锥的高是圆柱高的3倍，圆锥的容积等于圆柱的容积，正好装满；圆锥与长方体D比较，长方体的容积 = 长×宽×高，与圆锥的体积不会相等。 方法二：圆锥的容积：$V=\frac{1}{3}\pi\times6^{2}\times24 = 288\pi(cm^{3})$； 容器A的容积：$V=\pi\times6^{2}\times24 = 864\pi(cm^{3})$； 容器B的容积：$V=\pi\times2^{2}\times24 = 96\pi(cm^{3})$； 容器C的容积：$V=\pi\times6^{2}\times8 = 288\pi(cm^{3})$； 容器D的容积：$V = 6\times6\times8 = 288(cm^{3})$。 （2）结论： 将圆锥形容器中的水倒入容器C中，恰好能装满。