《2025年作业本江西教育出版社六年级数学下册人教版》

1. 选一选。
(1)把一个圆柱的底面分成许多相等的扇形，然后沿高把圆柱竖直切开，拼起来会得到一个近似的长方体。
①这个长方体与圆柱相比，( )不变，( )变了。
A. 体积 B. 表面积
②圆柱的底面积和长方体的底面积( )，圆柱的高和长方体的高( )。
A. 不相等 B. 相等
(2)圆柱和长方体的体积都可以用( )来计算。
A. $V = Sh$ B. $V=\pi r^{2}h$ C. $V = abh$
(3)等底等高的长方体和圆柱的体积相比，( )。
A. 长方体的体积大 B. 圆柱的体积大 C. 一样大

答案： 1. 选一选。 （1）把一个圆柱的底面分成许多相等的扇形，然后沿高把圆柱竖直切开，拼起来会得到一个近似的长方体。 ①这个长方体与圆柱相比，（A）不变，（B）变了。 A. 体积 B. 表面积 ②圆柱的底面积和长方体的底面积（B），圆柱的高和长方体的高（B）。 A. 不相等 B. 相等 （2）圆柱和长方体的体积都可以用（A）来计算。 A. $V = Sh$ B. $V=\pi r^{2}h$ C. $V = abh$ （3）等底等高的长方体和圆柱的体积相比，（C）。 A. 长方体的体积大 B. 圆柱的体积大 C. 一样大

2. 计算下面各圆柱的体积。
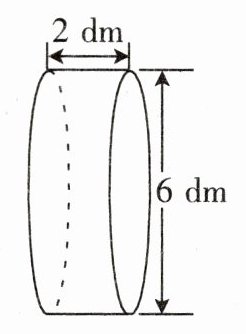
(1)

(2)

答案： （1）$V=\pi r^{2}h=3.14×3^{2}×8 = 226.08(cm^{3}) $
（2） $V=\pi r^{2}h=3.14×(6÷2)^{2}×2 = 56.52(dm^{3})$

3. 一根圆柱形的钢材，长150 cm，横截面的半径是5 cm，求这根钢材的体积。

答案： $V=\pi r^{2}h = 3.14×5^{2}×150$ $=11775(cm^{3})$

4. 一个圆柱，它的底面周长是31.4 cm，高是10 cm，它的体积是多少？

答案： $r = 31.4÷2÷3.14 = 5(cm)$ $V = 3.14×5^{2}×10 = 785(cm^{3})$

5. 水是生命之源，人体一天的饮水量应不少于1500 mL。小雨每天用底面内直径是6 cm、内高10 cm的圆柱形水杯喝6满杯水。小雨每天的饮水量达到要求了吗？（请写出计算过程）

答案： $6÷2 = 3(cm)$ $3.14×3^{2}×10×6 = 1695.6(cm^{3}) = 1695.6(mL)$ $1695.6 mL＞1500 mL$ 小雨每天的饮水量达到了要求。