《2024年孟建平单元测试九年级数学全一册人教版》

7. 关于 $x$ 的方程 $\left|\frac{x^{2}}{x - 1}\right|=a$ 仅有两个不同的实根,则实数 $a$ 的取值范围是( )
A. $a＞0$
B. $a\geqslant4$
C. $2 ＜ a ＜ 4$
D. $0 ＜ a ＜ 4$

答案： D 解析：当x - 1＜0，即x＜1时，方程化为x² + ax - a = 0(a≥0)①，则Δ₁ = a² + 4a≥0，
∴此方程必有实根；当x - 1＞0，即x＞1时，方程化为x² - ax + a = 0(a≥0)②，Δ₂ = (-a)² - 4a = a² - 4a.
∵原方程仅有两个不同的实根，当Δ₁ = 0时，方程①②具有相同的根，x = 0，不符合题意，
∴Δ₁＞0，即方程①应具有两个不同的实根，
∴方程②无实根，Δ₂＜0.
∴在a＞0的前提下，a² - 4a＜0，
∴0＜a＜4.

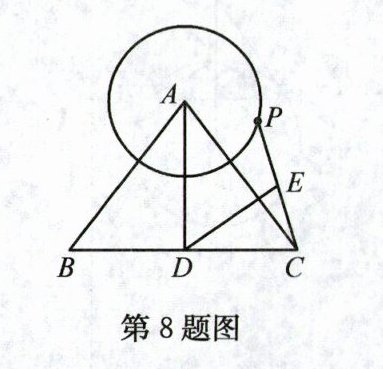
8. 如图,$\triangle ABC$ 中,$AB = AC$,$BC = 6$,$AD\perp BC$ 于点 $D$,$AD = 4$,$P$ 是半径为2的 $\odot A$ 上一动点,连接 $PC$,若 $E$ 是 $PC$ 的中点,连接 $DE$,则 $DE$ 长的最大值为( )
A. 3 B. 3.5 C. 4 D. 4.5

答案：
B 解析：
∵AB = AC，BC = 6，AD⊥BC，
∴BD = DC = $\frac{1}{2}$BC = 3.
∵E是PC中点，
∴DE//BP，DE = $\frac{1}{2}$BP，
∴当BP最大时，DE最大. 如图，当点P为BA延长线与⊙A的交点时，BP的长最大.
∵在Rt△ABD中，BD = 3，AD = 4，
∴BA = 5.
∵AP = 2，
∴BP = BA + AP = 7，
∴DE = $\frac{1}{2}$BP = 3.5.

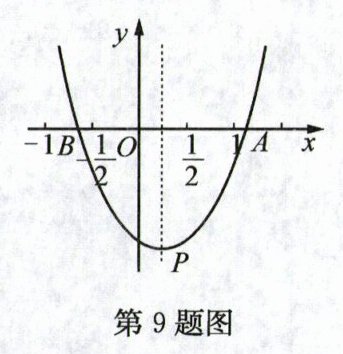
9. 如图,抛物线 $y = ax^{2}+bx + c(a,b,c$ 是常数,$a\neq0)$ 与 $x$ 轴交于 $A,B$ 两点,顶点 $P(m,n)$,给出下列结论：
① $2a + c＞0$;
②若点 $(-\frac{3}{2},y_{1}),(-\frac{1}{2},y_{2}),(\frac{1}{2},y_{3})$ 在抛物线上,则 $y_{1}＞y_{2}＞y_{3}$;
③若关于 $x$ 的方程 $ax^{2}+bx + k = 0$ 有实数根,则 $k＞c - n$;
④当 $n = -\frac{1}{a}$ 时,$\triangle ABP$ 为等腰直角三角形.
其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个

答案：
C 解析：
∵0＜ -$\frac{b}{2a}$＜$\frac{1}{2}$，a＞0，
∴a＞ -b.
∵x = -1时，y＞0，
∴a - b + c＞0，
∴2a + c＞a - b + c＞0，①正确；若(-$\frac{3}{2}$，y₁)，(-$\frac{1}{2}$，y₂)，($\frac{1}{2}$，y₃)在抛物线上，由图象可知，y₁＞y₂＞y₃，②正确；
∵抛物线与直线y = t有交点时，方程ax² + bx + c = t有解，且t≥n，
∴ax² + bx + c - t = 0有实数解. 要使得ax² + bx + k = 0有实数解，则k = c - t≤c - n，③错误；设抛物线的对称轴交x轴于点H.
∵$\frac{4ac - b²}{4a}$ = -$\frac{1}{a}$，
∴b² - 4ac = 4，
∴x = $\frac{-b±2}{2a}$，
∴|x₁ - x₂| = $\frac{2}{a}$，
∴AB = 2PH.
∵BH = AH，
∴PH = BH = AH，
∴△PAB是Rt△.
∵PA = PB，
∴△PAB是等腰Rt△，④正确. 故正确结论有3个.

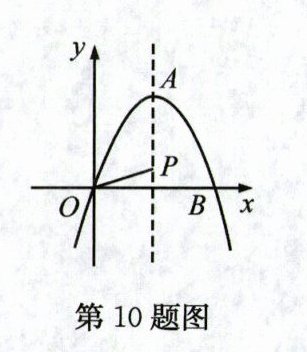
10. 如图,在平面直角坐标系中,抛物线 $y = -x^{2}+2\sqrt{3}x$ 的顶点为 $A$ 点,且与 $x$ 轴的正半轴交于点 $B$,$P$ 点为该抛物线对称轴上一点,则 $OP+\frac{1}{2}AP$ 的最小值为( )
A. $\frac{3 + 2\sqrt{21}}{4}$ B. $\frac{3 + 2\sqrt{3}}{2}$ C. 3 D. $2\sqrt{3}$

答案：
C 解析：如图，连接AO，AB，PB，作PH⊥OA于点H，BC⊥AO于点C. 令 -x² + 2√3x = 0，解得x = 0或x = 2√3，
∴点B(2√3，0)，
∴OB = 2√3.
∵y = -x² + 2√3x = -(x - √3)² + 3，
∴点A(√3，3)，
∴OA = √((√3)² + 3²) = 2√3. 根据对称性得AB = AO = 2√3，
∴AB = AO = OB，
∴△AOB为等边三角形，
∴∠OAP = 30°，
∴PH = $\frac{1}{2}$AP.
∵AP垂直平分OB，
∴PO = PB，
∴OP + $\frac{1}{2}$AP = PB + PH. 当H，P，B三点共线时，PB + PH的值最小，为BC的长.
∵Rt△ABC中，∠ABC = $\frac{1}{2}$∠ABO = 30°，
∴AC = $\frac{1}{2}$AB = √3，
∴BC = √(AB² - AC²) = 3，
∴OP + $\frac{1}{2}$AP的最小值为3. 点评：本题考查二次函数的性质、勾股定理的应用、等边三角形的判定与性质以及最短路径的解决方法，将OP + $\frac{1}{2}$AP转化为PB + PH，确定H，P，B三点共线时，PB + PH的值最小为BC的长是解决本题的关键.

11. 直角坐标系中,点 $(a,-3)$ 关于原点的对称点是 $(1,b - 1)$,则 $a + b=$______.

答案： 3

12. 关于 $x$ 的方程 $x^{2}-mx + n = 0$,若 $m + n = -1$,则方程的一个根为______.

答案： x = -1