2024年孟建平单元测试九年级数学全一册人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2024年孟建平单元测试九年级数学全一册人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第83页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
21. (10分)如图,⊙O的半径为1,A,P,B,C是⊙O上的四个点,∠APC = ∠CPB = 60°.
(1)判断△ABC的形状:__________;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于$\overset{\frown}{AB}$的什么位置时,四边形APBC的面积最大? 求出最大面积.
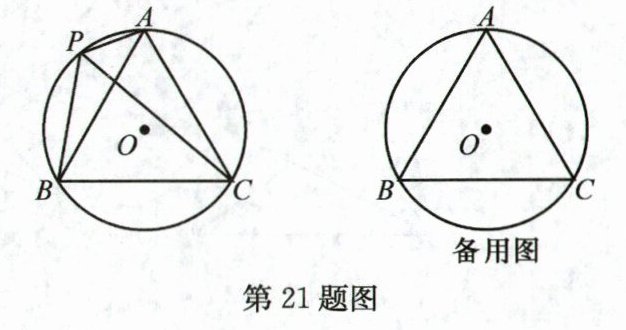
(1)判断△ABC的形状:__________;
(2)试探究线段PA,PB,PC之间的数量关系,并证明你的结论;
(3)当点P位于$\overset{\frown}{AB}$的什么位置时,四边形APBC的面积最大? 求出最大面积.

答案:
解:
(1)等边三角形
(2)CP = BP + AP. 证明:如图,在PC上截取PD = AP.
∵∠APC = 60°,
∴△APD是等边三角形,
∴AD = AP = PD,∠ADP = 60°,
∴∠ADC = 120°.
∵∠APB = ∠APC + ∠BPC = 120°,
∴∠APB = ∠ADC,又
∵∠ABP = ∠ACD,AP = AD,
∴△APB≌△ADC,
∴BP = CD,
∴CP = CD + PD = BP + AP.
(3)当点P为$\overset{\frown}{AB}$的中点时,四边形APBC的面积最大. 理由如下:如图,过点P作PE⊥AB于点E,过点C作CF⊥AB于点F.
∵S△APB = $\frac{1}{2}$AB·PE,S△ABC = $\frac{1}{2}$AB·CF,
∴S四边形APBC = $\frac{1}{2}$AB·(PE + CF),当点P为$\overset{\frown}{AB}$的中点时,PE + CF = PC,PC为⊙O的直径,
∴此时四边形APBC的面积最大.
∵⊙O的半径为1,
∴其内接正三角形的边长AB = $\sqrt{3}$,PC = 2,
∴S四边形APBC = $\frac{1}{2}\times\sqrt{3}\times2=\sqrt{3}$. 点评:本题主要考查了圆周角定理、等边三角形的判定、全等三角形的判定与性质以及三角形面积的计算等,
(2)题采用“截长法”添加辅助线构造全等三角形,
(3)题的关键是判断出四边形APBC面积最大时点P的位置.
解:
(1)等边三角形
(2)CP = BP + AP. 证明:如图,在PC上截取PD = AP.
∵∠APC = 60°,
∴△APD是等边三角形,
∴AD = AP = PD,∠ADP = 60°,
∴∠ADC = 120°.
∵∠APB = ∠APC + ∠BPC = 120°,
∴∠APB = ∠ADC,又
∵∠ABP = ∠ACD,AP = AD,
∴△APB≌△ADC,
∴BP = CD,
∴CP = CD + PD = BP + AP.
(3)当点P为$\overset{\frown}{AB}$的中点时,四边形APBC的面积最大. 理由如下:如图,过点P作PE⊥AB于点E,过点C作CF⊥AB于点F.
∵S△APB = $\frac{1}{2}$AB·PE,S△ABC = $\frac{1}{2}$AB·CF,
∴S四边形APBC = $\frac{1}{2}$AB·(PE + CF),当点P为$\overset{\frown}{AB}$的中点时,PE + CF = PC,PC为⊙O的直径,
∴此时四边形APBC的面积最大.
∵⊙O的半径为1,
∴其内接正三角形的边长AB = $\sqrt{3}$,PC = 2,
∴S四边形APBC = $\frac{1}{2}\times\sqrt{3}\times2=\sqrt{3}$. 点评:本题主要考查了圆周角定理、等边三角形的判定、全等三角形的判定与性质以及三角形面积的计算等,
(2)题采用“截长法”添加辅助线构造全等三角形,
(3)题的关键是判断出四边形APBC面积最大时点P的位置.

22. (12分)如图,⊙O是Rt△ABC的外接圆,直径AC = 4,过点C作⊙O的切线,与AB延长线交于点D,M为CD中点,连接BM,OM,且BC与OM相交于点N.
(1)求证:BM与⊙O相切;
(2)当∠BAC = 60°时,求弦AB和$\overset{\frown}{AB}$所夹图形的面积;
(3)在(2)的条件下,在$\overset{\frown}{AB}$上取一点F,使得∠ABF = 15°,连接OF,交弦AB于点H,求FH的长度.

(1)求证:BM与⊙O相切;
(2)当∠BAC = 60°时,求弦AB和$\overset{\frown}{AB}$所夹图形的面积;
(3)在(2)的条件下,在$\overset{\frown}{AB}$上取一点F,使得∠ABF = 15°,连接OF,交弦AB于点H,求FH的长度.

答案:
解:
(1)证明:连接OB.
∵⊙O是Rt△ABC的外接圆,
∴∠DBC = ∠ABC = 90°. 在Rt△DBC中,M为CD的中点,
∴BM = MC,
∴∠MBC = ∠MCB.
∵OB = OC,
∴∠OCB = ∠OBC.
∵CD为⊙O的切线,
∴∠ACD = ∠MCB + ∠OCB = ∠MBC + ∠OBC = 90°,即OB⊥BM,又
∵OB为⊙O的半径,
∴BM与⊙O相切.
(2)
∵∠BAC = 60°,OA = OB,
∴△ABO为等边三角形,
∴∠AOB = 60°.
∵AC = 4,
∴OA = 2,
∴弦AB和$\overset{\frown}{AB}$所夹图形的面积为S扇形AOB - S△AOB = $\frac{60\pi\times2^{2}}{360}-\frac{1}{2}\times2\times\sqrt{3}=\frac{2\pi}{3}-\sqrt{3}$.
(3)当∠ABF = 15°时,∠AOF = 2∠ABF = 30°,
∴等边△ABO中,OF平分∠AOB,
∴OF⊥AB. 在Rt△AOH中,AO = 2,∠AOH = 30°,
∴AH = 1,
∴OH = $\sqrt{3}$,
∴FH = 2 - $\sqrt{3}$. 点评:本题属于圆的综合问题,考查了圆周角定理、切线的判定与性质、等边三角形的判定与性质以及扇形的面积公式等,熟练掌握相关知识并灵活运用是解题的关键.
(1)证明:连接OB.
∵⊙O是Rt△ABC的外接圆,
∴∠DBC = ∠ABC = 90°. 在Rt△DBC中,M为CD的中点,
∴BM = MC,
∴∠MBC = ∠MCB.
∵OB = OC,
∴∠OCB = ∠OBC.
∵CD为⊙O的切线,
∴∠ACD = ∠MCB + ∠OCB = ∠MBC + ∠OBC = 90°,即OB⊥BM,又
∵OB为⊙O的半径,
∴BM与⊙O相切.
(2)
∵∠BAC = 60°,OA = OB,
∴△ABO为等边三角形,
∴∠AOB = 60°.
∵AC = 4,
∴OA = 2,
∴弦AB和$\overset{\frown}{AB}$所夹图形的面积为S扇形AOB - S△AOB = $\frac{60\pi\times2^{2}}{360}-\frac{1}{2}\times2\times\sqrt{3}=\frac{2\pi}{3}-\sqrt{3}$.
(3)当∠ABF = 15°时,∠AOF = 2∠ABF = 30°,
∴等边△ABO中,OF平分∠AOB,
∴OF⊥AB. 在Rt△AOH中,AO = 2,∠AOH = 30°,
∴AH = 1,
∴OH = $\sqrt{3}$,
∴FH = 2 - $\sqrt{3}$. 点评:本题属于圆的综合问题,考查了圆周角定理、切线的判定与性质、等边三角形的判定与性质以及扇形的面积公式等,熟练掌握相关知识并灵活运用是解题的关键.
查看更多完整答案,请扫码查看


