《2024年孟建平单元测试九年级数学全一册人教版》

10. 如图,AB是$\odot O$的直径,点P在BA的延长线上,弦CD交AB于点E,连接OD,PC,BC,$\angle AOD = 2\angle ABC$,$\angle P = \angle D$,过点E作弦$GF\perp BC$,交$\odot O$于G,F两点,连接CF,BG. 则下列结论:①$CD\perp AB$;②PC是$\odot O$的切线;③$OD// GF$;④弦CF的弦心距等于$\frac{1}{2}BG$. 其中正确的是 ( )


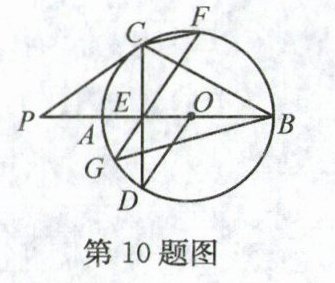
A. ①②④
B. ③④
C. ①②③
D. ①②③④

答案： 10. A 解析：
∵∠AOD为$\widehat{AD}$的圆心角，∠ABC为$\widehat{AC}$的圆周角，且∠AOD = 2∠ABC，
∴$\widehat{AC}=\widehat{AD}$.
∵AB为⊙O直径，
∴CD⊥AB，①正确；连接OC，由①得CD⊥AB，
∴∠P + ∠PCE = 90°.
∵∠P = ∠D = ∠DCO，
∴∠DCO + ∠PCE = 90°，
∴OC⊥CP，
∴PC是⊙O的切线，②正确；若OD//GF，则∠FEO = ∠EOD，
∵$\widehat{AC}=\widehat{AD}$，
∴∠FEO = ∠EOD = 2∠ABC，
∵GF⊥BC，
∴∠FEO + ∠ABC = 3∠ABC = 90°，
∴∠ABC = 30°，但题目未给出∠ABC的度数，③错误；连接AG，AC，过点O作OQ⊥CF于点Q，OH⊥BG于点H.
∵AB为直径，
∴∠ACB = 90°.
∵EF⊥BC，
∴AC//EF，
∴$\widehat{CF}=\widehat{AG}$，
∴CF = AG.
∵OQ⊥CF，OH⊥BG，
∴CQ = $\frac{1}{2}$AG，OH = $\frac{1}{2}$AG，BH = $\frac{1}{2}$BG，
∴OH = CQ.
∵OC = OB，∠OQC = ∠OHB = 90°，
∴Rt△OCQ≌Rt△BOH，
∴OQ = BH = $\frac{1}{2}$BG，④正确. 综上，正确的是①②④. 点评：本题是圆的综合题，考查了垂径定理及其推论、切线的判定、等腰三角形的性质、平行线的性质、全等三角形的判定与性质，解答本题的关键是熟练掌握圆的有关知识点.

11. 已知一个点到圆上的点的最大距离是6,最小距离是1,则这个圆的直径是______.

答案： 7或5

12. 当点$A(1,2)$,$B(3, - 3)$,$C(m,n)$三点可以确定一个圆时,m,n需要满足的条件是______.

答案： 5m + 2n≠9 解析：设直线AB的解析式为y = kx + b. 把A(1，2)，B(3， - 3)代入得$\begin{cases}2 = k + b\\-3 = 3k + b\end{cases}$，解得$\begin{cases}k = -\frac{5}{2}\\b = \frac{9}{2}\end{cases}$，
∴$l_{AB}:y = -\frac{5}{2}x+\frac{9}{2}$，
∵A，B，C三点能确定一个圆，
∴点C不在直线AB上，
∴$n≠-\frac{5}{2}m+\frac{9}{2}$，即5m + 2n≠9.

13. 如图,在扇形CAB中,$CD\perp AB$,垂足为D,$\odot E$是$\triangle ACD$的内切圆,连接AE,BE,则$\angle AEB$的度数为______.

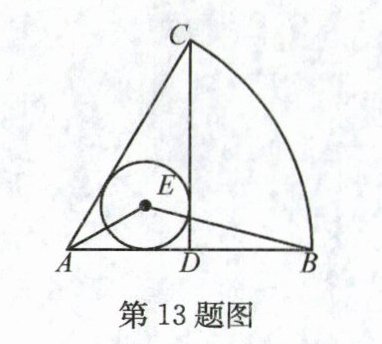
答案： 135° 解析：连接EC.
∵E是△ADC的内心，
∴易得∠AEC = 180° - $\frac{1}{2}$(∠DAC + ∠ACD) = 135°. 在△AEC和△AEB中，$\begin{cases}AE = AE\\\angle EAC = \angle EAB\\AC = AB\end{cases}$，
∴△EAC≌△EAB，
∴∠AEB = ∠AEC = 135°.

14. 如图,公园内有一个半径为20米的圆形草坪,A,B是圆上的点,O为圆心,$\angle AOB = 120^{\circ}$,从A到B只有路$\overset{\frown}{AB}$,一部分市民为走“捷径”,踩坏了花草,走出了一条小路AB. 通过计算可知,这些市民其实仅仅少走了______步. (假设1步为0.5米,$\sqrt{3}\approx1.732$,$\pi$取3.142,结果保留整数)

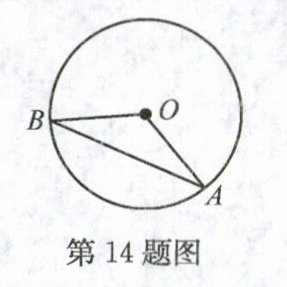
答案： 14. 15 解析：过点O作OC⊥AB于点C，则AC = BC，
∵∠AOB = 120°，OA = OB，
∴∠A = 30°，
∴OC = $\frac{1}{2}$OA = 10，
∴AC = $10\sqrt{3}$，
∴AB = $20\sqrt{3}$，又
∵$l_{\widehat{AB}}=\frac{120\pi\times20}{180}=\frac{40}{3}\pi$，
∴$\frac{40}{3}\pi - 20\sqrt{3}\approx7.25$米≈15步.

15. 如图,已知$\odot O$的半径为5,弦AB,CD所对的圆心角分别是$\angle AOB$,$\angle COD$,且$\angle AOB$与$\angle COD$互补,弦$CD = 8$,则弦AB的长为______.

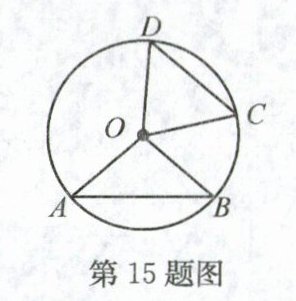
答案：
15. 6 解析：如图，延长AO交⊙O于点E，连接BE，则∠AOB + ∠BOE = 180°，又
∵∠AOB + ∠COD = 180°，
∴∠BOE = ∠COD，
∴BE = CD = 8.
∵AE为⊙O的直径，半径为5，
∴∠ABE = 90°，AE = 10，
∴AB = $\sqrt{AE^{2}-BE^{2}}=\sqrt{10^{2}-8^{2}} = 6$.

16. 如图,矩形ABCD中,$AB = 8$,$BC = 6$,$E$为BC边上一点,且$BE = 2$,$F$为AB上一点,$FG\perp AE$,分别交AE,CD于点P,G,以PC为直径的圆交线段FG于点Q,若$PF = QG$,则$BF =$______.

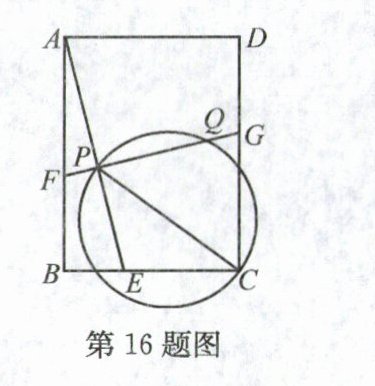
答案：
16. $\frac{13}{4}$ 解析：如图，连接AC交FG于点O，连接CQ，延长AE交圆于点H，连接CH，EF.
∵AB = 8，BC = 6，BE = 2，
∴EC = 4，AC = 10，AE = $2\sqrt{17}$.
∵PF = QG，易证得△AFP≌△CGQ，
∴AP = CQ，同理易证得△APO≌△CQO，
∴AO = CO = $\frac{1}{2}$AC = 5，PO = QO. 设QC = x，则OQ = $\sqrt{OC^{2}-QC^{2}}=\sqrt{25 - x^{2}}$. 易证四边形PHCQ为矩形，
∴HC = PQ = 2OQ = $2\sqrt{25 - x^{2}}$，PH = QC = x. 在Rt△EHC中，EH² = EC² - CH² = 16 - 4(25 - x²) = 4x² - 84.
∴AH = AE + EH = $2\sqrt{17}+\sqrt{4x^{2}-84}=2x$，解得$x = \frac{19\sqrt{17}}{17}$. 设BF = y，则FE² = BF² + BE² = y² + 4，
∴FP² = FE² - PE² = y² + 4 - $(2\sqrt{17}-\frac{19\sqrt{17}}{17})^{2}=y^{2}-\frac{157}{17}$，
∴AF² = FP² + AP² = y² - $\frac{157}{17}+(\frac{19\sqrt{17}}{17})^{2}=y^{2}+12$.
∵AF + BF = AB，
∴$\sqrt{y^{2}+12}+y = 8$，即y² + 12 = (8 - y)²，解得$y = \frac{13}{4}$，即BF = $\frac{13}{4}$. 点评：本题主要考查矩形的性质、圆周角定理、全等三角形的判定与性质、勾股定理等，解题的关键是熟练掌握相关的性质定理，能够添加常用辅助线构造全等三角形解决问题，属于中考中的压轴题.