《2024年孟建平单元测试九年级数学全一册人教版》

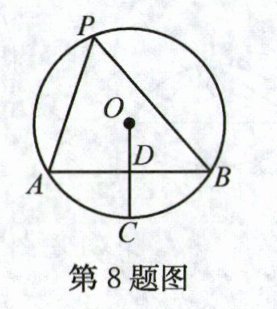
8. 如图,在⊙O中,AB为弦,OC⊥AB于点D,且OD=DC,P为⊙O上任意一点(A,B除外),连接PA,PB,若⊙O的半径为1,则S△PAB的最大值为 ( )


A. 1
B. $\frac{2\sqrt{3}}{3}$
C. $\frac{3\sqrt{3}}{4}$
D. $\frac{3\sqrt{3}}{2}$

答案：
解析:如图，连接OA,OB,延长CO交⊙O于点P',当点P在点P'处时，△PAB
　　　的面积最大.
∵OC⊥AB,
∴AD=$\frac{1}{2}$AB.
∵OA=OC=1,OD=DC,
∴OD=$\frac{1}{2}$OA
　　　=$\frac{1}{2}$,
∴AD=$\frac{\sqrt{3}}{2}$,
∴AB=2AD=√3,又
∵DP'=OD+OP'=$\frac{3}{2}$,
∴
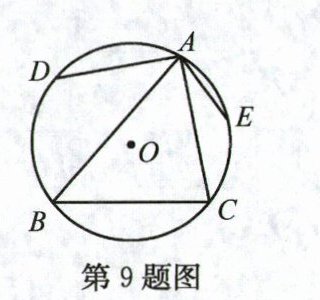
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 SPAB的最大值为$\frac{1}{2}$×$\frac{3}{2}$x$\sqrt{3}$=$\frac{3\sqrt{3}}{4}$

9. 如图,锐角△ABC内接于⊙O,点D,E分别是$\overset{\frown}{AB}$,$\overset{\frown}{AC}$的中点,设∠BAC=α,∠DAE=β,则 ( )


A. α+β=180°
B. 2β-α=180°
C. β-α=60°
D. 2α-β=60°

答案： 解析:连接DE,DC,BE.
∵D,E分别是AB,A⌒C的中点，
∴AD=BD,AE=CE,
∴∠ACD=∠BCD =∠AED,同理得∠ABE=∠EBC=∠ADE,
∴∠ACB=2∠AED,∠ABC=2∠ADE;在△ADE中,∠DAE=β,
∴∠ADE+∠AED=180°−β.
∴∠ABC+∠ACB=2(∠ADE+∠AED)=360°−2β.在△ABC中,∠BAC+∠ABC+∠ACB=180°,即α+360°−2β=180°,整理得2β−α=180°.

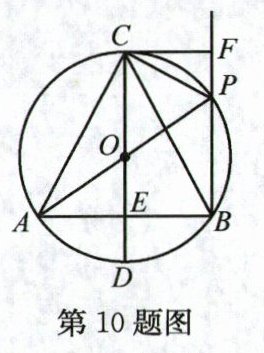
10. 如图,在⊙O中,直径CD垂直弦AB于点E,且OE=DE.点P为$\overset{\frown}{BC}$上一点(点P不与点B,C重合),连接AP,BP,CP,AC,BC,过点C作CF⊥BP延长线于点F,给出下列结论：
①△ABC是等边三角形;②在点P从B→C的运动过程中,$\frac{CF}{AP - BP}$的值始终等于$\frac{\sqrt{3}}{2}$,则
以上结论正确的是 ( )


A. ①②
B. ①
C. ②
D. 都不正确

答案：
解析:如图,过点C作CM⊥AP于点M,连接AD.
∵AE⊥OD,OE=DE,
∴
　　　OA=AD.
∵OA=OD,
∴OA=AD=OD,
∴△AOD是等边三角形，
∴∠ABC=
　　　∠D=60°.
∵CD⊥AB,
∴AE=EB,
∴CA=CB,
∴△ABC是等边三角形，故①正
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 确;
∵∠CPA=∠ABC=60°,∠APB=∠ACB=60°,
∴∠CPF=180°−∠APC−
　　　∠APB=60°°,
∴∠CPM=∠CPF.
∵CF⊥PF,CM⊥PA,
∴∠CFP=∠CVIP=
　　　90°,CF=CM.叉
∵PC=PC,
∴Rt△CPF≌Rt△CPM(HL),
∴PF=PM,CM=
CF.
∵AC=BC,∠AMC=∠CFB=90°,
∴Rt△AMC≌Rt△BFC(HL),
∴AM=
BF,
∴AP−PB=PM+AM−(BF−PF)=2PF.在Rt△CPF申,
∵∠CPF=60°,∠CFP=90°,
∴∠FCP=30°,
∴CP=2PF,
∴CF=√3PF,
∴$\frac{CF}{PA−PB}$=$\frac{\sqrt{3}}{2}$,②正确.

11. 90°的圆周角所对的弦是______.

答案： 直径

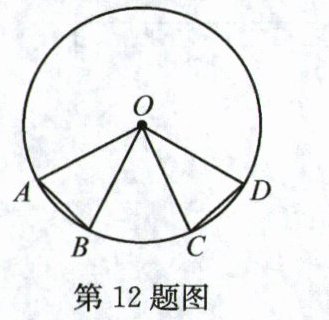
12. 在⊙O中有两个三角形:△AOB和△COD,点A,B,C,D依次在⊙O上,如图所示. 若这两个三角形关于过点O的直线l成轴对称,则点B关于直线l的对称点是______.

答案： 点C

13. 我国东汉初年的数学典籍《周髀算经》中总结了对几何工具“矩”(即直角形状的曲尺,如图1所示)的使用之道,其中就有“环矩以为圆”的方法. 我国许多数学家对该方法作了如下更具体的描述:如图2所示,在平面内固定两个钉子A,B,保持“矩”的两边始终紧靠两钉子的内侧,转动“矩”,则“矩”的顶点C的运动路线将会是一个圆. 依此描述,请用你学过的一个数学概念或定理解释“环矩以为圆”这种方法的道理:______________________________.

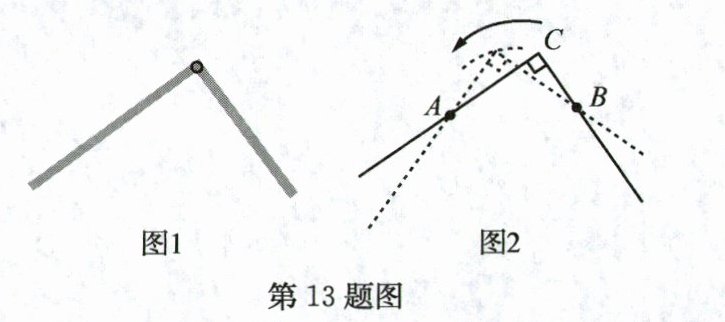
答案： 圆是所有到定点的距离等于定长的点的集合