《2024年孟建平单元测试九年级数学全一册人教版》

15. 如图,在△ABC中,∠BAC = 45°,AB = 4 cm,将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′,则阴影部分的面积为______.

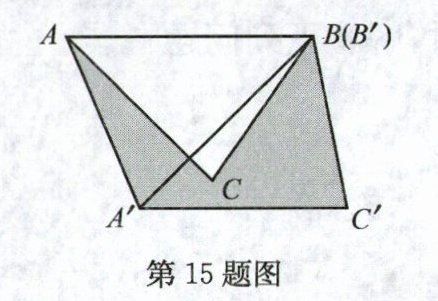
答案： 解析:由旋转可得S△ACB=SA'CB,A'B=AB=4.过点A'作A'M⊥AB于点M,则AVM=
　　　2$\sqrt{2}$
∴SAA'B=$\frac{1}{2}$×4×2$\sqrt{2}$=4$\sqrt{2}$,S影=S边形ACβ’−SACB=S边形AA'c'B'一S△A'CB=S△AA'B=
　　　4$\sqrt{2}$　　点评;本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前后的图形全等,运用面积的和差解决不规则图形的面积是解决此题的关键

16. 如图,在矩形ABCD中,AB = 8,BC = 6,将矩形ABCD绕点A逆时针旋转得到矩形AEFG,AE,FG分别交射线CD于点P,H,连接AH. 若点P是CH的中点,则△APH的周长为______.

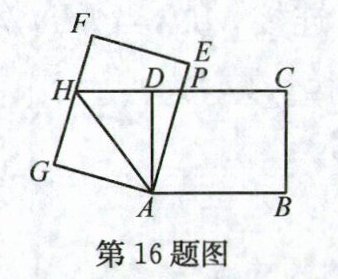
答案： 解析;设HD=x,由题意得HC=x+8.
∵点P是CH的中点，
∴HP=$\frac{8+x}{2}$=4+$\frac{1}{2}$x.由题图可知，在△HPA中，边HP上的高和边AP上的高相等，
∴由面积法可得AP=HP=4+$\frac{1}{2}$x.
∵
DP=HP−HD=4−$\frac{1}{2}$x,
∴在Rt△APD中,AP²=DP²+AD²,即(4+$\frac{1}{2}$x)²=(4−$\frac{1}{2}$x)²+6²,
解得x=$\frac{9}{2}$
∴AP=HP=4+$\frac{1}{2}$×$\frac{9}{2}$=$\frac{25}{4}$.在Rt△ADH申,HA=√HD²+AD²=　$\sqrt{(\frac{9}{2})+6²}$
　　　=$\frac{15}{2}$
∴CAPH=$\frac{15}{2}$+$\frac{25}{4}$×2=20.

17. (8分)(1)如图1,在正方形网格中,每个小正方形的边长均为1个单位. 将△ABC绕点C逆时针旋转90°,得到△A′B′C′,请你画出△A′B′C′(不要求画法);
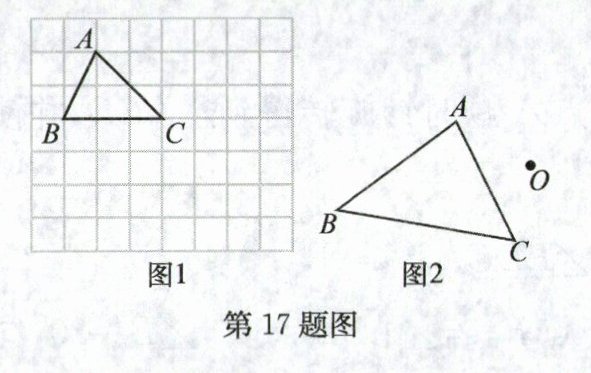
(2)如图2,已知点O和△ABC,试画出与△ABC关于点O成中心对称的图形.

答案： 略.

18. (8分)如图,把△ABC绕点B按逆时针方向旋转得到△DBE,已知点D,B,C在同一直线上,且∠ABE = ∠D. 求证:△ABC是等腰三角形.

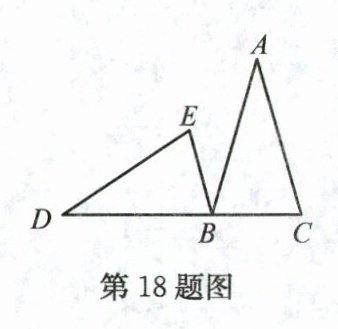
答案： 证明:由旋转得∠A=∠D,∠ABC=∠DBE
∵∠ABE=∠D,
∴∠A=∠ABE,,
∴BE//AC,
∴∠ACB=∠DBE,
∴∠ACB=∠ABC,
∴AB=AC,即△ABC是等腰三角形,

19. (10分)如图,菱形ABCD的顶点A,D在直线l上,∠BAD = 60°,以点A为旋转中心将菱形ABCD顺时针旋转α(0° ＜ α ＜ 30°),得到菱形AB′C′D′,B′C′交对角线AC于点M,C′D′交直线l于点N,连接MN,当MN//B′D′时,解答下列问题.
(1)求证:△AB′M≌△AD′N;
(2)求α的大小.

答案： 解:
(1)证明:
∵四边形AB{C'D'是菱形，
∴AB’=B'C'=C'D'=AD'.
∵∠B'C'D'=∠B'AD'=
　　　∠BAD=60°,
∴△AB'D',△B'C'D'是等边三角形.
∵MN//B'D',
∴∠C'MN=∠CB'D'=60°,∠CNM=∠CD'B'=60°,叉
∵∠MC'N=∠B'C'D'=60°,
∴△CMN是等边三角形，
∴C'VI=
C'N,
∴MB'=ND',又
∵∠AB'M=∠AD'N,AB'=AD',
∴△AB'M≌△AD'N(SAS).　　
(2)由△AB'M≌△AD'N得∠B3AM=∠DAN.
∵∠B{AD'=60°,∠CAD=$\frac{1}{2}$∠BAD=30°,
∴∠D'AN =∠BAM=$\frac{1}{2}$(∠BAD'−∠CAD)=15°,即α=15°.