《2024年孟建平单元测试九年级数学全一册人教版》

22.(10分)关于$x$的方程$x^{2}+(2k - 1)x + k^{2}-1 = 0$有两个实数根$x_{1},x_{2}$.
(1)求实数$k$的取值范围;
(2)若$x_{1},x_{2}$满足$x_{1}^{2}+x_{2}^{2}=16 + x_{1}x_{2}$,求实数$k$的值.

答案： 解:
(1)
∵关于x的方程x²+(2k−1)x+k²−1=0有两个实数根x1,x2,
∴△=(2k−1)²−4(k²−1)=−4k+5≥0,解得k≤$\frac{5}{4}$.　
(2)由题意得x+x2=1−2k,x1x2=k²−1.
∵x²+x²=(x+x2)²−2xx2=16+xx2,
∴(1−2k)²−2(k²−1)=16+(k²−1),即k²−4k−12=0,解得k=−2或k=6 (不合题意，舍去)，
∴实数k的值为−2.　点评:本题考查了一元二次方程根与系数的关系以及根的判别式，解题的关键是:
(1)根据方程根的判别式，找出△=−4k+5≥0;
(2)根据根与系数的关系，结合x²+x2=16+x1x2,找出关于k的一元二次方程.

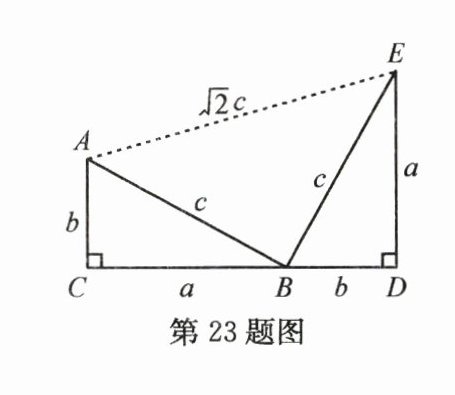
23.(12分)如图,四边形$ACDE$是证明勾股定理时用到的一个图形,$a,b,c$是$Rt\triangle ABC$和$Rt\triangle BED$的边长,易知$AE=\sqrt{2}c$,这时我们把关于$x$的形如$ax^{2}+\sqrt{2}cx + b = 0$的一元二次方程称为“勾系一元二次方程”,比如$3x^{2}+5\sqrt{2}x + 4 = 0$是“勾系一元二次方程”.请解决下列问题:

(1)试判断方程$x^{2}+2x + 1 = 0$______“勾系一元二次方程”(填“是”或“不是”);
(2)若$x=-1$是“勾系一元二次方程”$ax^{2}+\sqrt{2}cx + b = 0$的一个根,且四边形$ACDE$的周长是12,求$\triangle ABC$的面积.

答案： 解:
(1)是　解析:方程x²+2x+1=0中,
∵a=1,b=1,
∴c=√2,.　$\sqrt{2}$c=√2×$\sqrt{2}$=2,
∴方程x²+2x +1=0是“勾系一元二次方程”.　　
(2)当x=−1时，有α一$\sqrt{2}$c+b=0,即a+b=$\sqrt{2}$c.
∵四边形ACDE的周长是12,
∴2a+2b+　$\sqrt{2}$c=12,即2(a+b)+　　$\sqrt{2}$c=12,
∴3$\sqrt{2}$c=12,
∴c=2√2,
∴a+b=$\sqrt{2}$c=4,a²+b²=c²=8.
∵(a+b)²=a²+2ab+b²,
∴ab=4,
∴SABC=$\frac{1}{2}$ab=2.