《2024年孟建平单元测试九年级数学全一册人教版》

8. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知$\angle A = 90^{\circ},BD = 4,CF = 6$,则正方形$ADOF$的边长是( )


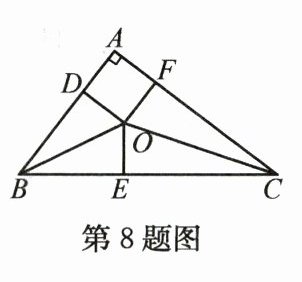
A. $\sqrt{2}$
B. 2
C. $\sqrt{3}$
D. 4

答案： 解析:设正方形ADOF的边长为x,由题意得BE=BD=4,CE:=CF=6,
∴BC=BE+CE=10.在Rt△ABC中,AC²+AB²=BC²,即(6+x)²+(x+4)²=10²,整理得x²+10x−24=0,解得x=2或x =−12(舍去),
∴正方形ADOF的边长是2.

9. 已知关于$x$的一元二次方程$(a + 1)x^{2}+2x+(a + 1)=0$有两个相等的实数根,下列判断正确的是( )
A. 1一定不是关于$x$的方程$x^{2}+x + a = 0$的根
B. 0一定不是关于$x$的方程$x^{2}+x + a = 0$的根
C. 1和-1都是关于$x$的方程$x^{2}+x + a = 0$的根
D. 1和-1不都是关于$x$的方程$x^{2}+x + a = 0$的根

答案： 解析:由题意可得a+1≠0,
∴a≠−1.
∵该一元二次方程有两个相等的实数根，
∴△=2²−4(a+1)²=0,
∴(a+1)²=1,解得a=0或a=−2,
∴x²+x+a=0化为x²+x=0或x²+x−2=0,解得x =0或x=−1或x=−2或x=1.

10. 已知关于$x$的方程$x^{2}+5px + 10 = 0$和$x^{2}-2x - 25p = 0$有公共根,则$p$的值为( )
A. $-\frac{2}{5}$
B. $\frac{7}{5}$
C. $-\frac{2}{5}$或$\frac{7}{5}$
D. $-\frac{2}{5}$或$-\frac{7}{5}$

答案： 解析:
∵方程x²+5px+10=0①和x²−2x−25p=0②有公共根,
∴①−②得,5px+2x+25p+10=0,因式分解得(5p+2)(x+5)=0,解得p=一$\frac{2}{5}$,x=−5.当p=−$\frac{2}{5}$时,得x²−2x+10=0,△=4−4×1×10=−36＜0,方程无解，舍去;当x=−5时,代入方程x²+5px+10=0可得25−25p +10=0,解得p=$\frac{7}{5}$.把p=$\frac{7}{5}$代入x²+5px+10=0得,x²+7x+10=0,解得x=−5,x2=−2;把p=$\frac{7}{5}$代入x²−2x−25p=0得,x²−2x−35=0,解得x=−5,x2=7.
∴两方程有公共根x=−5，符合题意.故的值为$\frac{7}{5}$

11. 关于$x$的方程$(m^{2}-m - 2)x^{2}+mx + 1 = 0$是一元二次方程,则$m$的取值范围是______.

答案： m≠−1且m≠2　解析:
∵方程为一元二次方程，
∴m²一m−2≠0,解得m≠2且m≠−1.

12. 已知$m$是一元二次方程$x^{2}+4x - 3 = 0$的一个根,则代数式$3m^{2}+12m - 2$的值为______.

答案： 7

13. 设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比等于下部与全部(全身)的高度比,可以增加视觉美感,按此比例,如果雕像的高为2 m,那么上部应设计为多高?设雕像的上部高$x$m,列方程,并化成一般形式是__________.

答案： x²−6.x+4=0　解析:
∵雕像上部高xm,
∴下部高(2−x)m,
∵雕像的上部(腰以上)与下部(腰以下)的高度比等于下部与全部(全身)的高度比，,
∴$\frac{x}{2−x}$=$\frac{2−x}{2}$,化为一般式是x²−6x+4=0.

14. 已知关于$x$的方程$(a - 1)x^{2}-2x + 1 = 0$有实数根,则$a$的取值范围是______.

答案： a≤2　解析:当a≠1时方程有实数根,则△=4−4(a−1)≥0,解得a≤2;当a=1时,方程为−2x+1=0,仍有实数根.综上,a≤2.

15. 已知关于$x$的一元二次方程$mx^{2}-(m + 2)x+\frac{m}{4}=0$有两个不相等的实数根$x_{1},x_{2}$,若$\frac{1}{x_{1}}+\frac{1}{x_{2}}=4m$则$m$的值是______.

答案： 2　解析:根据题意可得x十x2=$\frac{m+2}{m}$,1×2=$\frac{1}{4}$
∴1+$\frac{1}{2}$=x2x+1xx21=$\frac{4(m+2)}{m}$=4m,解得m=2 或m=−1.又
∵△=[−(m+2)]²−4m.$\frac{m}{4}$＞0,解得m＞−1,
∴m=2.

16. 在平面直角坐标系$xOy$中,过原点$O$及点$A(0,2),C(6,0)$作矩形$OABC$,$\angle AOC$的平分线交$AB$于点$D$. 点$P$从点$O$出发,以每秒$\sqrt{2}$个单位长度的速度沿射线$OD$方向移动;同时点$Q$从点$O$出发,以每秒2个单位长度的速度沿$x$轴正方向移动. 设移动时间为$t$秒,当$t$为______时,$\triangle PQB$为直角三角形.

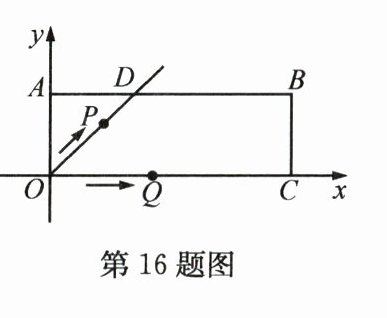
答案： 2或5i　$\sqrt{5}$　解析:由题可知,B(6,2),P(t,t),Q(2t,，0),,
∴BP²=(6−t)²+(2−t)²,BQ²=(2t−6)²+2²,PQ²=t²+t²=2t².①当BP²+BQ²=PQ²时,(6−t)²+(2−t)²²+(2t−6)²+2²=2t²,解得t=5±　　$\sqrt{5}$;②当BQ²+PQ²=BP²时,(2t−6)²+2²+2t²=(6−t)²+(2−t)²,解得t=2或0(舍去);③当BP²+PQ²=BQ²时,(6−t)²+(2−t)²+2t²=(2t−6)²+2²,解得t=0(舍去).综上,t=2或5 ±$\sqrt{5}$　　点评:本题涉及动点问题，考查了勾股定理的运用、矩形的性质以及一元二次方程的应用，解答本题关键是设出P，Q两点的坐标，由题意建立方程从而求出符合题意的t值，同时要运用数形结合的思想，难度较大.