《2024年孟建平单元测试九年级数学全一册人教版》

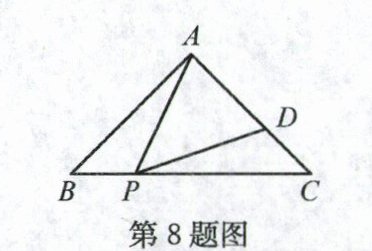
8. 如图,等腰Rt△ABC的直角边长为3,P为斜边BC上一点,且BP = 1,D为AC上一点,若∠APD = 45°,则CD的长为 ( )


A. $\frac{5}{3}$
B. $\frac{2\sqrt{3}-1}{3}$
C. $\frac{3\sqrt{2}-1}{3}$
D. $\frac{3}{5}$

答案： 解析:
∵△ABC为等腰Rt△,
∴∠B=∠C=45°,
∴∠BAP+∠BPA=135°,
∵∠APD=45°,
∴
　　∠DPC+∠BPA=135°,
∴∠DPC=∠BAP,
∴△BAP∽△CPD,
∴$\frac{CD}{BP}$=A.
∵等腰Rt△ABC中，,
AC=AB=3,
∴BC=3√2,
∵BP=1,
∴PC=3√2−1,
∴CD=$\frac{PC.BP}{BA}$=$\frac{3\sqrt{2}−1}{3}$.　点评:本题主要
　　　考查相似三角形的判定与性质，解题的关键是能根据已知条件快速判断出∠DPC=∠BAP，进而得
　　到一组相似三角形求解,

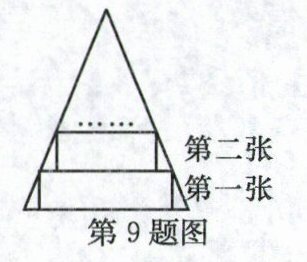
9. 如图,一张等腰三角形纸片,底边长18 cm,底边上的高为18 cm,现沿底边依次从下往上裁剪宽度均为3 cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是 ( )


A. 第4张
B. 第5张
C. 第6张
D. 第7张

答案： 解析:由题意得正方形的边长为3.设从三角形顶角的顶点到正方形顶部的距离为x，则小正方形
　　顶部的边与原三角形两腰所围三角形必与原三角形相似，
∴$\frac{3}{18}$=$\frac{x}{18}$,解得x=3.
∴该小三角形底边
　　到原三角形底边的距离为18−3=15,15÷3=5,
∴这张正方形纸条是第5张.

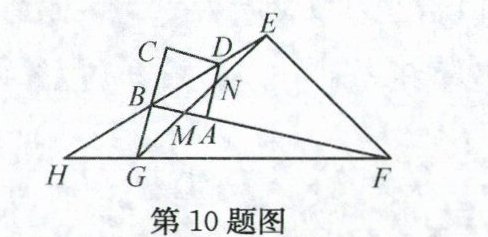
10. 如图,正方形ABCD的对角线BD的延长线上有一点E,且$\frac{BD}{DE}=\frac{3}{2}$,点G在CB延长线上,连接EG,过点E作FE⊥EG,交BA的延长线于点F,连接FG并延长,交DB的延长线于点H. 若AB = 3,BG = 3,则下列结论:①EG = EF;②∠BEG = ∠BFG;③△HBF∽△GBE;④$BH=\frac{39\sqrt{2}}{10}$,其中正确的个数是 ( )


A. 4个
B. 3个
C. 2个
D. 1个

答案： 解析:在△BMG和△EMF中,∠MBG=∠MEF=90°,∠BMG=∠EMF,
∴△BMG∽△EMF,
　
∴MMBE_−MMGF,即EME_=MMGB,又
∵∠BME=∠GMF，,
∴△BME∽△GMF,
∴∠MGF=∠MBE=45°,,
　　　∠BEG=∠BFG;
∵∠GEF=90°,
∴△GEF为等腰Rt△,
∴EG=EF,①②正确;
∵∠BEG=
　　　∠BFG,∠HBF=∠GBE=135°,
∴△HBF∽△GBE,③正确;过点G作GP⊥BH于点P,易得
　　　△PBG为等腰Rt△,
∴PB=PG,PB²+PG²=BG²,且BG=3,
∴2PB²=9,
∴PG=PB=$\frac{3\sqrt{2}}{2}$.同
　　　理，在等腰Rt△ABD中可得BD=3$\sqrt{2}$
∵$\frac{BD}{DE}$=$\frac{3}{2}$
∴DE=2$\sqrt{2}$
∴BE=5$\sqrt{2}$,
∴PE=PB+BD+
DE=13242,
∴GE=√PG²+PE=$\sqrt{89}$4
∵△GEF为等腰Rt△,
∴∠EGF=45°,
∴∠HGE=135°.
　　　又
∵∠HBF=135°,
∴∠HGE=∠HBF,且∠BEG=∠GEH,
∴△BEG∽△GEH,
∴$\frac{B}{E}$=$\frac{GE}{HE}$,
∴
　　　　　　　　　　2
　　　HE=$\frac{GE"}{BE}$=$\frac{\sqrt{89}}{5\sqrt{2}}$=$\frac{89√2}{10}$
∴BH=HE−BE=$\frac{39\sqrt{2}}{10}$,④正确.综上，正确的共有4个.

11. 若△ADE∽△ACB,且$\frac{AD}{AC}=\frac{2}{3}$,DE = 10,则BC = ______.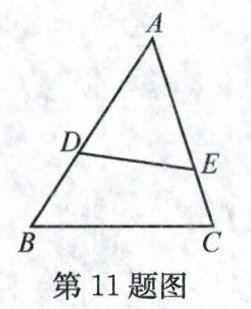

答案： 15

12. 图中的两个四边形相似,则$x + y =$______,α = ______.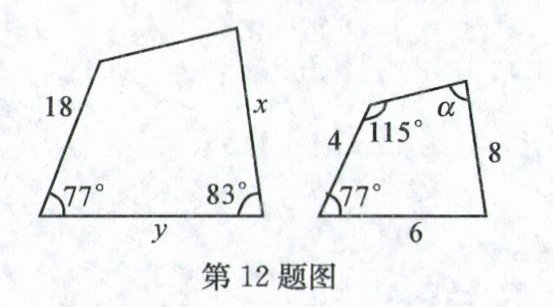

答案： 63　85°

13. 如图,已知点E(-6,2),F(-1,-1),以点O为位似中心,按1∶2的比例把△EFO缩小,则点E的对应点的坐标为______.

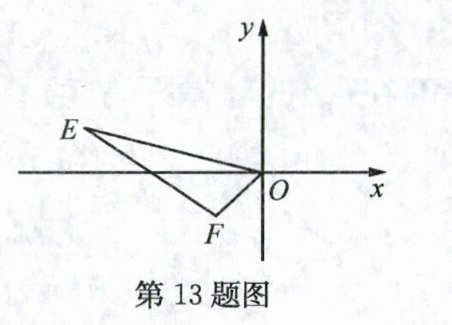
答案： (−3,1)或(3,−1)

14. 如图,若△ABC内一点P满足∠PAC = ∠PCB = ∠PBA,则称点P为△ABC的布罗卡尔点,三角形的布罗卡尔点是法国数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮. 已知△ABC中,CA = CB,∠ACB = 120°,P为△ABC的布罗卡尔点,若PB = 3,则PA + PC = ______.

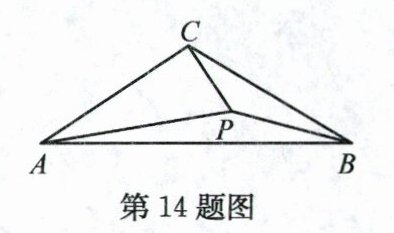
答案： 4$\sqrt{3}$　解析:过点C作CH⊥AB于H.
∵CA=CB,CH⊥AB,∠ACB=120°,
∴AH=BH,∠ACH=
　　　∠BCH=60°,∠CAB=∠CBA=30°,
∴BC=2CH,
∴AB=2BH=2　$\sqrt{BC²−(\frac{1}{2}BC)}$=√3BC;
∵
　　　∠PAC=∠PCB=∠PBA,
∴∠PAB=∠PBC,
∴△PAB∽△PBC,
∴$\frac{PA}{PB}$=$\frac{PB}{PC}$=$\frac{AB}{BC}$=√3.
∵PB=
　　　3,
∴PA=3$\sqrt{3}$,PC=√3,
∴PA+PC=4$\sqrt{3}$

15. 李明用一张矩形纸片玩折纸游戏. 如图1,将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,然后把纸片展平;如图2,将图1中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD上的点C'处,点B落在点B'处,得到折痕EF,B'C'交AB于点M,C'F交DE于点N. 已知AB = 4,AD = 3,则$\frac{MC'}{C'F}$的值为______.

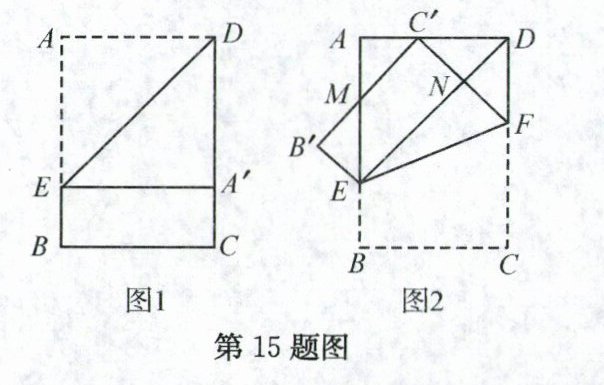
答案： $\frac{2}{3}$　解析:连接CE.由题图1得四边形AEA'D是正方形，四边形EBCA'是矩形，
∴AE=A'E,A'E
　　　=BC,
∴AE=BC.
∵四边形ABCD是矩形,AB=4,AD=3,
∴∠A=∠B=90°=∠ADC,AD=BC,
　
∴BE=4−3=1,∠AC'M+∠AMC=90°,由题图2可得∠B=∠B=90°=∠B'C'F,B'E=BE=
　　　1,
∴∠A=∠B{=90°,∠AC'M+∠DC'F=90°,，
∴∠AMC'=∠DC'F,
∴△AMC∽△DC'F,
∴
　　　=$\frac{AC'}{DF}$.在Rt△ACE和Rt△BEC'申,
∵AE=B'C',CE=EC,
∴Rt△ACE≌Rt△B'EC'(HL),
∴
AC=B'E=1.
∴CD=AD−AC=2,设DF=x,则C'F=CF=4−x.在Rt△DCF中,CD²²+DF²
　　　=C'F²,
∴22+x²=(4−x)²,解得x=$\frac{3}{2}$,...MCFC−−$\frac{AC'}{DF}$=$\frac{1}{3}$=$\frac{2}{3}$.