1 [2024·河南商丘月考]若直角三角形的两直角边长分别为$\sqrt{3}$,$\sqrt{6}$,则此直角三角形的面积为( )
A. 3
B. $3\sqrt{2}$
C. $\frac{3\sqrt{2}}{2}$
D. $\frac{3}{2}$
A. 3
B. $3\sqrt{2}$
C. $\frac{3\sqrt{2}}{2}$
D. $\frac{3}{2}$
答案:
C
2 若一直角三角形两直角边的长分别为$\sqrt{2}$,$\sqrt{6}$,则该直角三角形斜边上的中线长为________.
答案:
$\sqrt{2}$
3 如图,某校自行车棚的人字架棚顶为等腰三角形ABC,D是边AB的中点,中柱CD = $2\sqrt{6}$,AB = $2\sqrt{3}$,求△ABC的周长及面积.


答案:
解:在等腰三角形$ABC$中,$\because D$是边$AB$的中点,$CD$是中柱,$CD = 2\sqrt{6}$,$AB = 2\sqrt{3}$,
$\therefore CD\perp AB$,$AD = BD = \sqrt{3}$,
$\therefore$在$Rt\triangle ACD$中,$AC = \sqrt{AD^{2}+CD^{2}} = 3\sqrt{3}$,
$\therefore BC = 3\sqrt{3}$,
$\therefore \triangle ABC$的周长为$3\sqrt{3}+3\sqrt{3}+2\sqrt{3} = 8\sqrt{3}$,
面积为$\frac{1}{2}\times2\sqrt{3}\times2\sqrt{6} = 6\sqrt{2}$.
$\therefore CD\perp AB$,$AD = BD = \sqrt{3}$,
$\therefore$在$Rt\triangle ACD$中,$AC = \sqrt{AD^{2}+CD^{2}} = 3\sqrt{3}$,
$\therefore BC = 3\sqrt{3}$,
$\therefore \triangle ABC$的周长为$3\sqrt{3}+3\sqrt{3}+2\sqrt{3} = 8\sqrt{3}$,
面积为$\frac{1}{2}\times2\sqrt{3}\times2\sqrt{6} = 6\sqrt{2}$.
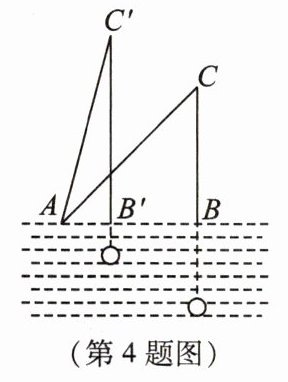
4 [2023·浙江杭州上城区期中]如图,已知钓鱼竿AC的长为6 m,露在水面上的鱼线BC的长为$3\sqrt{2}$ m,某钓者想看看鱼钩的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C'的长为$\sqrt{34}$ m,则BB'的长为( )
A. $\sqrt{2}$ m B. $2\sqrt{2}$ m C. $\sqrt{5}$ m D. $2\sqrt{3}$ m
A. $\sqrt{2}$ m B. $2\sqrt{2}$ m C. $\sqrt{5}$ m D. $2\sqrt{3}$ m

答案:
B
5 如图,斜面AC的坡比为1∶2,AC = $3\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端点B与点A有一条彩带相连. 若AB = 10米,则旗杆BC的高度为( )
A. 5米 B. 6米 C. 8米 D. $(3+\sqrt{5})$米

A. 5米 B. 6米 C. 8米 D. $(3+\sqrt{5})$米

答案:
A
6(PISA试题)[2023·浙江温州期中]有一块长方形木板,木工采用如图的方式,在木板上截出两个面积分别为18 dm²和32 dm²的正方形木板,则剩余木料(阴影部分)的面积为________dm².


答案:
6
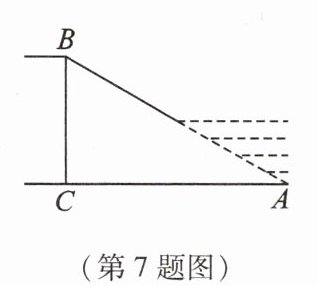
7 链教材P19课内练习第1题改编 如图,河坝横断面迎水坡AB的坡比是1∶$\sqrt{3}$(坡比是坡面的铅直高度BC与水平宽度AC之比),水平宽度AC = $3\sqrt{3}$米,则坡面AB的长度是________米.

答案:
6
查看更多完整答案,请扫码查看


