6 如图,△ABC的中线AF与中位线DE相交于点O.
(1)求证:AF与DE互相平分.
(2)当△ABC满足______时,四边形ADFE是正方形.

(1)求证:AF与DE互相平分.
(2)当△ABC满足______时,四边形ADFE是正方形.

答案:
(1)证明:
∵ △ABC的中线AF与中位线DE相交于点O,
∴ EF是△ABC的中位线,AD = BD,
∴ EF//AB,EF = $\frac{1}{2}$AB = AD,
∴ 四边形ADFE是平行四边形,
∴ AF与DE互相平分.
(2)AB = AC,∠BAC = 90°.
提示:由
(1),得四边形ADFE是平行四边形.
∵ AB = AC,AF是△ABC的中线,
∴ AF⊥BC.
∵ DE是△ABC的中位线,
∴ DE//BC,
∴ AF⊥DE,
∴ 平行四边形ADFE是菱形.
又
∵ ∠BAC = 90°,
∴ 四边形ADFE是正方形.
(1)证明:
∵ △ABC的中线AF与中位线DE相交于点O,
∴ EF是△ABC的中位线,AD = BD,
∴ EF//AB,EF = $\frac{1}{2}$AB = AD,
∴ 四边形ADFE是平行四边形,
∴ AF与DE互相平分.
(2)AB = AC,∠BAC = 90°.
提示:由
(1),得四边形ADFE是平行四边形.
∵ AB = AC,AF是△ABC的中线,
∴ AF⊥BC.
∵ DE是△ABC的中位线,
∴ DE//BC,
∴ AF⊥DE,
∴ 平行四边形ADFE是菱形.
又
∵ ∠BAC = 90°,
∴ 四边形ADFE是正方形.
7 小琦在复习几种特殊四边形的关系时整理如图,(1)(2)(3)(4)处需要添加条件,则下列条件添加错误的是 ( )
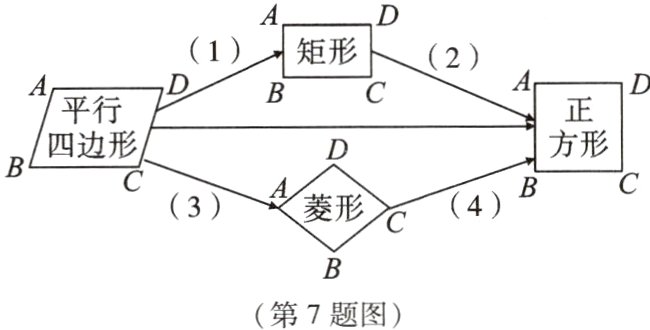
A. (1)处可填∠A=90°
B. (2)处可填AD=AB
C. (3)处可填DC=CB
D. (4)处可填∠B=∠D

A. (1)处可填∠A=90°
B. (2)处可填AD=AB
C. (3)处可填DC=CB
D. (4)处可填∠B=∠D
答案:
D 解析:A.有一个角是直角的平行四边形是矩形,
∴
(1)处可填∠A = 90°,此选项不符合题意;B.一组邻边相等的矩形是正方形,
∴
(2)处可填AD = AB,此选项不符合题意;C.一组邻边相等的平行四边形是菱形,
∴
(3)处可填DC = CB,此选项不符合题意;D.有一个角是直角的菱形是正方形,而∠B = ∠D无法判定有一个角是直角,此选项符合题意. 故选D.
∴
(1)处可填∠A = 90°,此选项不符合题意;B.一组邻边相等的矩形是正方形,
∴
(2)处可填AD = AB,此选项不符合题意;C.一组邻边相等的平行四边形是菱形,
∴
(3)处可填DC = CB,此选项不符合题意;D.有一个角是直角的菱形是正方形,而∠B = ∠D无法判定有一个角是直角,此选项符合题意. 故选D.
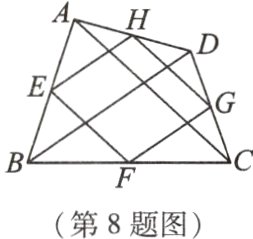
8 如图,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点. 有下列说法:①若AC=BD,则四边形EFGH是菱形;②若AC⊥BD,则四边形EFGH是矩形;③若四边形EFGH是平行四边形,则AC与BD互相平分;④若四边形EFGH是正方形,则AC与BD互相垂直且相等. 其中,正确的个数是 ( )
A. 1
B. 2
C. 3
D. 4

A. 1
B. 2
C. 3
D. 4
答案:
C 解析:
∵ E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,
∴ EF//AC//HG,EF = $\frac{1}{2}$AC = HG,
∴ 四边形EFGH是平行四边形,即当四边形EFGH是平行四边形时,四边形ABCD可为任意四边形,无法推出AC与BD互相平分,③错误;
∵ E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,
∴ EH//BD//GF,EH = $\frac{1}{2}$BD = GF,
∴ 当BD = AC时,EF = EH,
∴ 四边形EFGH是菱形,①正确;当AC⊥BD时,EF⊥EH,
∴ 四边形EFGH是矩形,②正确;当四边形EFGH是正方形时,EF = EH且EF⊥EH,此时AC = BD且AC⊥BD,④正确.
∴ 正确的说法为①②④,共3个. 故选C.
∵ E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,
∴ EF//AC//HG,EF = $\frac{1}{2}$AC = HG,
∴ 四边形EFGH是平行四边形,即当四边形EFGH是平行四边形时,四边形ABCD可为任意四边形,无法推出AC与BD互相平分,③错误;
∵ E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,
∴ EH//BD//GF,EH = $\frac{1}{2}$BD = GF,
∴ 当BD = AC时,EF = EH,
∴ 四边形EFGH是菱形,①正确;当AC⊥BD时,EF⊥EH,
∴ 四边形EFGH是矩形,②正确;当四边形EFGH是正方形时,EF = EH且EF⊥EH,此时AC = BD且AC⊥BD,④正确.
∴ 正确的说法为①②④,共3个. 故选C.
9 [2023·浙江同步练习]如图,在平行四边形ABCD中,对角线AC,BD相交于点O,并且∠DAC=60°,∠ADB=15°,E是AD上一动点,连接EO并延长交BC于点F. 在点E从点D向点A移动的过程中(点E与点D,A不重合),四边形AFCE的变化情况是 ( )

A. 平行四边形→矩形→平行四边形→菱形→平行四边形
B. 平行四边形→矩形→平行四边形→正方形→平行四边形
C. 平行四边形→菱形→平行四边形→矩形→平行四边形
D. 平行四边形→矩形→菱形→正方形→平行四边形

A. 平行四边形→矩形→平行四边形→菱形→平行四边形
B. 平行四边形→矩形→平行四边形→正方形→平行四边形
C. 平行四边形→菱形→平行四边形→矩形→平行四边形
D. 平行四边形→矩形→菱形→正方形→平行四边形
答案:
C 解析:
∵ 四边形ABCD是平行四边形,
∴ OA = OC,AD//BC,
∴ ∠ACF = ∠CAD. 又
∵ ∠COF = ∠AOE,
∴ △AOE≌△COF,
∴ AE = CF.
∵ AE//CF,
∴ 四边形AECF是平行四边形.
∵ ∠DAC = 60°,∠ADB = 15°,
∴ ∠AOD = 180° - 60° - 15° = 105°,
∴ 在点E从点D向点A移动的过程中,当∠AOE = 90°时,EF⊥AC,
∴ 平行四边形AECF是菱形.
当∠AEC = 90°时,平行四边形AECF是矩形,
∴ OE = OC,∠ACE = 30°,
∴ ∠OEC = 30°,
∴ ∠AOE = 2∠ACE = 60°,即当∠AOE = 60°时,平行四边形AECF是矩形.
综上所述,在点E从点D向点A移动的过程中(点E与点D,A不重合),四边形AFCE的变化情况是:平行四边形→菱形→平行四边形→矩形→平行四边形. 故选C.
∵ 四边形ABCD是平行四边形,
∴ OA = OC,AD//BC,
∴ ∠ACF = ∠CAD. 又
∵ ∠COF = ∠AOE,
∴ △AOE≌△COF,
∴ AE = CF.
∵ AE//CF,
∴ 四边形AECF是平行四边形.
∵ ∠DAC = 60°,∠ADB = 15°,
∴ ∠AOD = 180° - 60° - 15° = 105°,
∴ 在点E从点D向点A移动的过程中,当∠AOE = 90°时,EF⊥AC,
∴ 平行四边形AECF是菱形.
当∠AEC = 90°时,平行四边形AECF是矩形,
∴ OE = OC,∠ACE = 30°,
∴ ∠OEC = 30°,
∴ ∠AOE = 2∠ACE = 60°,即当∠AOE = 60°时,平行四边形AECF是矩形.
综上所述,在点E从点D向点A移动的过程中(点E与点D,A不重合),四边形AFCE的变化情况是:平行四边形→菱形→平行四边形→矩形→平行四边形. 故选C.
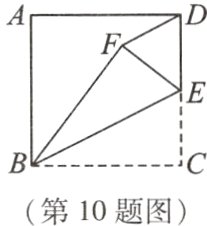
10 如图,在正方形ABCD中,AB=4,E是CD的中点,将△BCE沿BE翻折,得到△BFE,连接DF,则DF的长是 ( )
A. $\frac{\sqrt{5}}{5}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{3\sqrt{5}}{5}$
D. $\frac{4\sqrt{5}}{5}$

A. $\frac{\sqrt{5}}{5}$
B. $\frac{2\sqrt{5}}{5}$
C. $\frac{3\sqrt{5}}{5}$
D. $\frac{4\sqrt{5}}{5}$
答案:
D 解析:如答图,连接CF,交BE于点H.
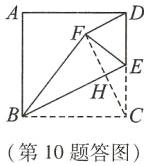
∵ 在正方形ABCD中,AB = 4,E是CD的中点,
∴ BC = CD = 4,CE = DE = 2,∠BCD = 90°,
∴ BE = $\sqrt{BC^{2}+CE^{2}}$ = $\sqrt{4^{2}+2^{2}}$ = 2$\sqrt{5}$.
∵ 将△BCE沿BE翻折,得到△BFE,
∴ EF = CE = 2,BE⊥CF,FH = CH.
∵ $S_{\triangle BCE}$ = $\frac{1}{2}$BE·CH = $\frac{1}{2}$BC·CE,
∴ CH = $\frac{BC·CE}{BE}$ = $\frac{4×2}{2\sqrt{5}}$ = $\frac{4\sqrt{5}}{5}$,
∴ EH = $\sqrt{CE^{2}-CH^{2}}$ = $\sqrt{2^{2}-(\frac{4\sqrt{5}}{5})^{2}}$ = $\frac{2\sqrt{5}}{5}$.
∵ CE = DE,FH = CH,
∴ DF = 2EH = $\frac{4\sqrt{5}}{5}$. 故选D.
D 解析:如答图,连接CF,交BE于点H.

∵ 在正方形ABCD中,AB = 4,E是CD的中点,
∴ BC = CD = 4,CE = DE = 2,∠BCD = 90°,
∴ BE = $\sqrt{BC^{2}+CE^{2}}$ = $\sqrt{4^{2}+2^{2}}$ = 2$\sqrt{5}$.
∵ 将△BCE沿BE翻折,得到△BFE,
∴ EF = CE = 2,BE⊥CF,FH = CH.
∵ $S_{\triangle BCE}$ = $\frac{1}{2}$BE·CH = $\frac{1}{2}$BC·CE,
∴ CH = $\frac{BC·CE}{BE}$ = $\frac{4×2}{2\sqrt{5}}$ = $\frac{4\sqrt{5}}{5}$,
∴ EH = $\sqrt{CE^{2}-CH^{2}}$ = $\sqrt{2^{2}-(\frac{4\sqrt{5}}{5})^{2}}$ = $\frac{2\sqrt{5}}{5}$.
∵ CE = DE,FH = CH,
∴ DF = 2EH = $\frac{4\sqrt{5}}{5}$. 故选D.
查看更多完整答案,请扫码查看


