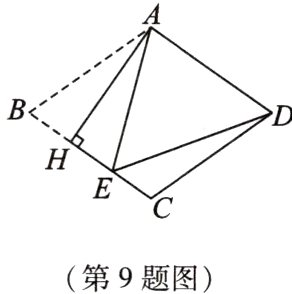
9. 如图,把菱形ABCD沿AH折叠,点B落在BC边上的点E处. 若∠BAE=40°,则∠EDC的大小为 ( )
A. 10°
B. 15°
C. 18°
D. 20°

A. 10°
B. 15°
C. 18°
D. 20°
答案:
9.B 解析
∵将菱形ABCD沿AH折叠,点B落在BC边上的点E处,
∴AB = AE.
∵∠BAE = 40°,
∴$∠B = ∠AEB=\frac{1}{2}×(180° - 40°)=70°$.
∵在菱形ABCD中,AB = AD,∠ADC = ∠B = 70°,AD//BC,
∴∠DAE = ∠AEB = 70°.
∵AB = AE,AB = AD,
∴AE = AD,
∴$∠ADE=\frac{1}{2}×(180° - ∠DAE)=\frac{1}{2}×(180° - 70°)=55°$,
∴∠EDC = ∠ADC - ∠ADE = 70° - 55° = 15°.故选B.
∵将菱形ABCD沿AH折叠,点B落在BC边上的点E处,
∴AB = AE.
∵∠BAE = 40°,
∴$∠B = ∠AEB=\frac{1}{2}×(180° - 40°)=70°$.
∵在菱形ABCD中,AB = AD,∠ADC = ∠B = 70°,AD//BC,
∴∠DAE = ∠AEB = 70°.
∵AB = AE,AB = AD,
∴AE = AD,
∴$∠ADE=\frac{1}{2}×(180° - ∠DAE)=\frac{1}{2}×(180° - 70°)=55°$,
∴∠EDC = ∠ADC - ∠ADE = 70° - 55° = 15°.故选B.
10. [2024·浙江金华期末]菱形的周长为32 cm,一个内角的度数是120°,则该菱形的面积为 ( )
A. 32√3 cm²
B. 16√3 cm²
C. 32 cm²
D. 16 cm²
A. 32√3 cm²
B. 16√3 cm²
C. 32 cm²
D. 16 cm²
答案:
10.A 解析如答图,菱形ABCD的周长为32cm,∠BAD = 120°,对角线AC,BD交于点E,
∴AB = BC = CD = AD = 32÷4 = 8 (cm),AC⊥BD,
∴∠AEB = 90°,∠BAE = $∠DAE=\frac{1}{2}∠BAD=\frac{1}{2}×120° = 60°$,
∴∠ABE = 90° - 60° = 30°,
∴$CE = AE=\frac{1}{2}AB=\frac{1}{2}×8 = 4$(cm),
∴AC = 8cm,
∴$DE = BE=\sqrt{AB^{2}-AE^{2}}=\sqrt{8^{2}-4^{2}} = 4\sqrt{3}$(cm),
∴$BD = 8\sqrt{3}$cm,
∴菱形ABCD的面积为$\frac{1}{2}AC\cdot BD=\frac{1}{2}×8×8\sqrt{3}=32\sqrt{3}$($cm^{2}$).故选A.

10.A 解析如答图,菱形ABCD的周长为32cm,∠BAD = 120°,对角线AC,BD交于点E,
∴AB = BC = CD = AD = 32÷4 = 8 (cm),AC⊥BD,
∴∠AEB = 90°,∠BAE = $∠DAE=\frac{1}{2}∠BAD=\frac{1}{2}×120° = 60°$,
∴∠ABE = 90° - 60° = 30°,
∴$CE = AE=\frac{1}{2}AB=\frac{1}{2}×8 = 4$(cm),
∴AC = 8cm,
∴$DE = BE=\sqrt{AB^{2}-AE^{2}}=\sqrt{8^{2}-4^{2}} = 4\sqrt{3}$(cm),
∴$BD = 8\sqrt{3}$cm,
∴菱形ABCD的面积为$\frac{1}{2}AC\cdot BD=\frac{1}{2}×8×8\sqrt{3}=32\sqrt{3}$($cm^{2}$).故选A.

11. (PISA试题)[2024·上海校级月考]如图,已知菱形ABCD的对角线AC,BD分别为6,8,点M是边BC的中点,点N是边CD上一点,点P是对角线BD上一点,则PM+PN的最小值为_______.


答案:
11.$\frac{24}{5}$ 解析如答图,作点M关于BD的对称点Q,连接NQ交BD于点P,连接MQ.
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP = ∠MBP,AB = BC,即Q在AB上,AB与CB关于BD成轴对称,
∴MQ⊥BD.
∵点M为BC的中点,
∴$BM = CM=\frac{1}{2}BC=\frac{1}{2}AB$,
∴$BQ = BM=\frac{1}{2}AB$,
∴Q为AB的中点.
∵N为CD上一动点,
∴当QN⊥CD时,QN最短,即$PM + PN = PQ + PN = QN$最短.
∵四边形ABCD是菱形,
∴$CO=\frac{1}{2}AC = 3$,$BO=\frac{1}{2}BD = 4$.在$Rt△BOC$中,$BC=\sqrt{CO^{2}+BO^{2}} = 5$.由等面积法可得$\frac{1}{2}×6×8 = 5QN$,
∴$QN=\frac{24}{5}$,
∴$PM + PN$的最小值为$\frac{24}{5}$.

11.$\frac{24}{5}$ 解析如答图,作点M关于BD的对称点Q,连接NQ交BD于点P,连接MQ.
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP = ∠MBP,AB = BC,即Q在AB上,AB与CB关于BD成轴对称,
∴MQ⊥BD.
∵点M为BC的中点,
∴$BM = CM=\frac{1}{2}BC=\frac{1}{2}AB$,
∴$BQ = BM=\frac{1}{2}AB$,
∴Q为AB的中点.
∵N为CD上一动点,
∴当QN⊥CD时,QN最短,即$PM + PN = PQ + PN = QN$最短.
∵四边形ABCD是菱形,
∴$CO=\frac{1}{2}AC = 3$,$BO=\frac{1}{2}BD = 4$.在$Rt△BOC$中,$BC=\sqrt{CO^{2}+BO^{2}} = 5$.由等面积法可得$\frac{1}{2}×6×8 = 5QN$,
∴$QN=\frac{24}{5}$,
∴$PM + PN$的最小值为$\frac{24}{5}$.

12. 如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DE//AC,且DE=1/2AC,连接CE,OE,连接AE交OD于点F.
(1)求证:OE=CD.
(2)若菱形ABCD的边长为8,∠ABC=60°,求AE的长.

(1)求证:OE=CD.
(2)若菱形ABCD的边长为8,∠ABC=60°,求AE的长.

答案:
(1)证明
∵四边形ABCD是菱形,
∴$OC=\frac{1}{2}AC$,$AC⊥BD$,
∴∠COD = 90°.
又
∵$DE=\frac{1}{2}AC$,
∴DE = OC.
又
∵DE//AC,
∴四边形OCED是平行四边形.
又
∵∠COD = 90°,
∴平行四边形OCED是矩形,
∴OE = CD.
(2)解
∵四边形ABCD是菱形,
∴AB = BC.
∵∠ABC = 60°,
∴△ABC是等边三角形,
∴AC = AB = 8,
∴AO = 4.
∴在矩形OCED中,$CE = OD=\sqrt{AD^{2}-AO^{2}} = 4\sqrt{3}$.
∵四边形DOCE为矩形,
∴∠OCE = 90°,
∴$AE=\sqrt{AC^{2}+CE^{2}}=\sqrt{8^{2}+(4\sqrt{3})^{2}} = 4\sqrt{7}$.
(1)证明
∵四边形ABCD是菱形,
∴$OC=\frac{1}{2}AC$,$AC⊥BD$,
∴∠COD = 90°.
又
∵$DE=\frac{1}{2}AC$,
∴DE = OC.
又
∵DE//AC,
∴四边形OCED是平行四边形.
又
∵∠COD = 90°,
∴平行四边形OCED是矩形,
∴OE = CD.
(2)解
∵四边形ABCD是菱形,
∴AB = BC.
∵∠ABC = 60°,
∴△ABC是等边三角形,
∴AC = AB = 8,
∴AO = 4.
∴在矩形OCED中,$CE = OD=\sqrt{AD^{2}-AO^{2}} = 4\sqrt{3}$.
∵四边形DOCE为矩形,
∴∠OCE = 90°,
∴$AE=\sqrt{AC^{2}+CE^{2}}=\sqrt{8^{2}+(4\sqrt{3})^{2}} = 4\sqrt{7}$.
13. 如图,在菱形ABCD中,AB=4,∠ABC=60°,P为AD边上任意一点(不包括端点),连接AC,过点P作PQ//AC交边CD于点Q,R为线段AC上的一点.
(1)若R为菱形ABCD的对角线的交点,PQ为△ACD的中位线,连接PR,QR,求PR+QR的值.
(2)当PR+QR的值最小时,请确定点R的位置,并求出PR+QR的最小值.
(3)当PR+QR+PQ的值最小时,在备用图中作出此时点P,Q的位置,写出作法并直接写出PR+QR+PQ的最小值.

(1)若R为菱形ABCD的对角线的交点,PQ为△ACD的中位线,连接PR,QR,求PR+QR的值.
(2)当PR+QR的值最小时,请确定点R的位置,并求出PR+QR的最小值.
(3)当PR+QR+PQ的值最小时,在备用图中作出此时点P,Q的位置,写出作法并直接写出PR+QR+PQ的最小值.

答案:
13.解
(1)
∵R为菱形ABCD的对角线的交点,
∴AD//BC,AB = AD = BC = CD,∠ADC = ∠ABC,AR = CR.
∵PQ为△ACD的中位线,AB = 4,
∴$AP=\frac{1}{2}AD=\frac{1}{2}AB = 2 = CQ$.
∵∠ADC = ∠ABC = 60°,AB = BC,AD = DC,
∴△ABC和△ACD都是等边三角形,
∴AC = 4,AR = CR = 2,∠DAC = ∠DCA = 60°,
∴△APR和△CQR都是等边三角形,
∴PR = AP = QR = CQ = 2,
∴PR + QR = 4.
(2)如答图
(1),作点Q关于AC的对称点Q',连接RQ',AQ',PC.
当P,R,Q'在同一条直线上且PQ'⊥BC时,PR + QR的值最小,即为PQ'的长.
易知AP = CQ = CQ',AP//CQ',
∴四边形AQ'CP为平行四边形,
∴R为AC的中点.
当PQ'⊥BC时,PQ'的长取得最小值,
此时将PQ'向左平移得到P'Q'',使点P'与点A重合,则$PQ' = P'Q''$.
由
(1)知△ABC是等边三角形,
∴BC = AB = 4,
∴$BQ''=\frac{1}{2}BC = 2$,
∴在$Rt△ABQ''$中,由勾股定理,得$P'Q'' = 2\sqrt{3}$,
∴当PR + QR的值最小时,R为AC的中点,PR + QR的最小值为$2\sqrt{3}$.

(3)如答图
(2),取AD的中点P,过点P作PQ//AC,则点P,Q即为所求.
PR + QR + PQ的最小值为6.
13.解
(1)
∵R为菱形ABCD的对角线的交点,
∴AD//BC,AB = AD = BC = CD,∠ADC = ∠ABC,AR = CR.
∵PQ为△ACD的中位线,AB = 4,
∴$AP=\frac{1}{2}AD=\frac{1}{2}AB = 2 = CQ$.
∵∠ADC = ∠ABC = 60°,AB = BC,AD = DC,
∴△ABC和△ACD都是等边三角形,
∴AC = 4,AR = CR = 2,∠DAC = ∠DCA = 60°,
∴△APR和△CQR都是等边三角形,
∴PR = AP = QR = CQ = 2,
∴PR + QR = 4.
(2)如答图
(1),作点Q关于AC的对称点Q',连接RQ',AQ',PC.
当P,R,Q'在同一条直线上且PQ'⊥BC时,PR + QR的值最小,即为PQ'的长.
易知AP = CQ = CQ',AP//CQ',
∴四边形AQ'CP为平行四边形,
∴R为AC的中点.
当PQ'⊥BC时,PQ'的长取得最小值,
此时将PQ'向左平移得到P'Q'',使点P'与点A重合,则$PQ' = P'Q''$.
由
(1)知△ABC是等边三角形,
∴BC = AB = 4,
∴$BQ''=\frac{1}{2}BC = 2$,
∴在$Rt△ABQ''$中,由勾股定理,得$P'Q'' = 2\sqrt{3}$,
∴当PR + QR的值最小时,R为AC的中点,PR + QR的最小值为$2\sqrt{3}$.

(3)如答图
(2),取AD的中点P,过点P作PQ//AC,则点P,Q即为所求.
PR + QR + PQ的最小值为6.
查看更多完整答案,请扫码查看


