1. 下列说法正确的是 ( )
A. 一组对边平行的四边形是平行四边形
B. 有一个角是直角的四边形是矩形
C. 四条边相等的四边形是菱形
D. 有一组邻边相等的四边形是菱形
A. 一组对边平行的四边形是平行四边形
B. 有一个角是直角的四边形是矩形
C. 四条边相等的四边形是菱形
D. 有一组邻边相等的四边形是菱形
答案:
C 解析A.两组对边平行的四边形是平行四边形,此选项说法错误;B.有一个角是直角的平行四边形是矩形,此选项说法错误;C.四条边相等的四边形是菱形,此选项说法正确;D.有一组邻边相等的四边形不一定是菱形,此选项说法错误.故选C.
2. 下列图形,不能用两个全等的含有30°角的直角三角形拼出的是 ( )
A. 腰与底边不相等的等腰三角形
B. 等边三角形
C. 矩形
D. 菱形
A. 腰与底边不相等的等腰三角形
B. 等边三角形
C. 矩形
D. 菱形
答案:
D 解析A.可以让两条较短的直角边重合,两条较长的直角边在一条直线上;B.可以让两条较长的直角边重合,两条较短的直角边在一条直线上;C.可以让两条斜边重合,两组相等的直角边组成两组对边;D.无法拼出.故选D.
3. 下列性质,菱形不一定具有的是 ( )
A. 对角线互相平分
B. 对角线互相垂直
C. 对角线相等
D. 既是轴对称图形又是中心对称图形
A. 对角线互相平分
B. 对角线互相垂直
C. 对角线相等
D. 既是轴对称图形又是中心对称图形
答案:
C 解析A.菱形的对角线互相平分,此选项不符合题意;B.菱形的对角线互相垂直,此选项不符合题意;C.菱形的对角线不一定相等,此选项符合题意;D.菱形既是轴对称图形又是中心对称图形,此选项不符合题意.故选C.
4. 链接教材P120作业题第4题改编(一题多解)[2024·浙江丽水中期中]如图,在菱形ABCD中,AE⊥BC于点E,AF⊥CD于点F. 若BE=EC,则∠EAF= ( )
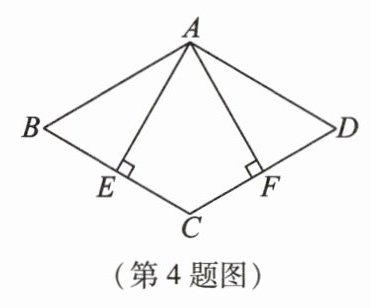
A. 75°
B. 60°
C. 50°
D. 45°

A. 75°
B. 60°
C. 50°
D. 45°
答案:
B 解析如答图,连接AC.
∵AE⊥BC,BE=EC,
∴AC=AB,∠AEC=90°.
∵四边形ABCD是菱形,
∴AB=BC,
∴AC=AB=BC,
∴△ABC是等边三角形,
∴∠B=60°,
∴∠BCD=120°.
∵AF⊥CD,
∴∠AFC=90°,
∴∠EAF=360°−90°−90°−120°=60°.故选B.
一题多解:如答图,连接AC.
∵AE⊥BC于点E,BE=CE,
∴AB=AC,∠BAE=∠CAE.
∵四边形ABCD为菱形,
∴AB=BC,
∴AB=BC=AC,
∴△ABC为等边三角形,
∴∠BAC=60°,
∴∠CAE=30°.同理,得∠CAF=30°,
∴∠EAF=60°.

B 解析如答图,连接AC.
∵AE⊥BC,BE=EC,
∴AC=AB,∠AEC=90°.
∵四边形ABCD是菱形,
∴AB=BC,
∴AC=AB=BC,
∴△ABC是等边三角形,
∴∠B=60°,
∴∠BCD=120°.
∵AF⊥CD,
∴∠AFC=90°,
∴∠EAF=360°−90°−90°−120°=60°.故选B.
一题多解:如答图,连接AC.
∵AE⊥BC于点E,BE=CE,
∴AB=AC,∠BAE=∠CAE.
∵四边形ABCD为菱形,
∴AB=BC,
∴AB=BC=AC,
∴△ABC为等边三角形,
∴∠BAC=60°,
∴∠CAE=30°.同理,得∠CAF=30°,
∴∠EAF=60°.

5. 如图,在平面直角坐标系xOy中,若菱形ABCD的顶点A,B的坐标分别为(-3,0),(2,0),点D在y轴上,则点C的坐标是_______.
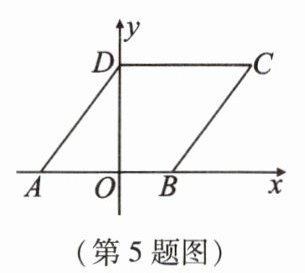

答案:
(5,4) 解析
∵点A,B的坐标分别为(−3,0),(2,0),
∴AO=3,OB=2.
∵四边形ABCD是菱形,
∴AD=CD=AB=5,
∴DO=$\sqrt{AD^{2}-AO^{2}}$=4,
∴点C的坐标是(5,4).
∵点A,B的坐标分别为(−3,0),(2,0),
∴AO=3,OB=2.
∵四边形ABCD是菱形,
∴AD=CD=AB=5,
∴DO=$\sqrt{AD^{2}-AO^{2}}$=4,
∴点C的坐标是(5,4).
6. 菱形ABCD的对角线AC=10,BD=8,则菱形ABCD的面积是 ( )
A. 80
B. 60
C. 40
D. 30
A. 80
B. 60
C. 40
D. 30
答案:
C 解析菱形ABCD的面积为$\frac{AC\cdot BD}{2}=\frac{10×8}{2}=40$.故选C.
【变式】[2024·河北沧州模拟]将矩形ABCD和菱形AFDE按如图放置,若图中矩形面积是菱形面积的2倍,则下列结论正确的是 ( )
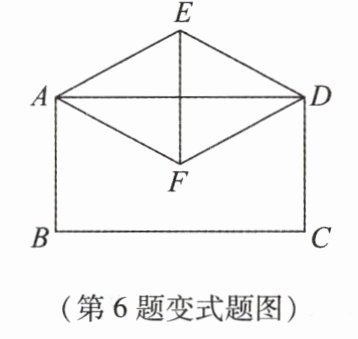
A. ∠EAF=60°
B. AB=AF
C. AD=2AB
D. AB=EF

A. ∠EAF=60°
B. AB=AF
C. AD=2AB
D. AB=EF
答案:
[变式]D 解析
∵$S_{矩形ABCD}=AD\cdot AB$,$S_{菱形AFDE}=\frac{1}{2}AD\cdot EF$,
∴$AD\cdot AB = 2×\frac{1}{2}AD\cdot EF$,
∴AB = EF.故选D.
∵$S_{矩形ABCD}=AD\cdot AB$,$S_{菱形AFDE}=\frac{1}{2}AD\cdot EF$,
∴$AD\cdot AB = 2×\frac{1}{2}AD\cdot EF$,
∴AB = EF.故选D.
7. 如图,菱形ABCD的边长为6,对角线相交于点O,面积为28,则该菱形的两条对角线的长度之和为_______.
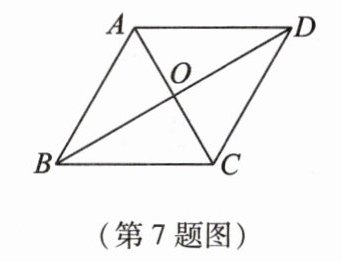

答案:
7.16 解析
∵四边形ABCD是菱形,
∴$AO = CO=\frac{1}{2}AC$,$DO = BO=\frac{1}{2}BD$,$AC⊥BD$.
∵菱形ABCD的面积为28,
∴$\frac{1}{2}AC\cdot BD = 2OD\cdot AO = 28$①.
∵菱形ABCD的边长为6,
∴$OD^{2}+OA^{2}=6^{2}$②.由①②两式可得$(OD + AO)^{2}=OD^{2}+OA^{2}+2OD\cdot AO = 6^{2}+28 = 64$,
∴$OD + AO = 8$(负值已舍去),
∴$2(OD + AO)=16$,即该菱形的两条对角线的长度之和为16.
∵四边形ABCD是菱形,
∴$AO = CO=\frac{1}{2}AC$,$DO = BO=\frac{1}{2}BD$,$AC⊥BD$.
∵菱形ABCD的面积为28,
∴$\frac{1}{2}AC\cdot BD = 2OD\cdot AO = 28$①.
∵菱形ABCD的边长为6,
∴$OD^{2}+OA^{2}=6^{2}$②.由①②两式可得$(OD + AO)^{2}=OD^{2}+OA^{2}+2OD\cdot AO = 6^{2}+28 = 64$,
∴$OD + AO = 8$(负值已舍去),
∴$2(OD + AO)=16$,即该菱形的两条对角线的长度之和为16.
8. 在菱形ABCD中,AC是对角线.
(1)如图(1),若AB=5,则菱形ABCD的周长为_______;若∠DAB=60°,则∠D的度数是_______,∠DCA的度数是_______.
(2)如图(2),P是AB上一点,连接DP交对角线AC于点E,连接EB,求证:∠APD=∠CBE.

(1)如图(1),若AB=5,则菱形ABCD的周长为_______;若∠DAB=60°,则∠D的度数是_______,∠DCA的度数是_______.
(2)如图(2),P是AB上一点,连接DP交对角线AC于点E,连接EB,求证:∠APD=∠CBE.

答案:
(1)20 120° 30°
提示:
∵四边形ABCD是菱形,
∴AB = BC = CD = AD = 5,
$∠DAB + ∠ADC = 180°$,$∠DCA=\frac{1}{2}∠DCB=\frac{1}{2}∠DAB$,
∴菱形ABCD的周长为$4×5 = 20$,$∠ADC = 120°$,$∠DCA = 30°$.
(2)证明
∵四边形ABCD是菱形,
∴DC//AB,DC = BC,∠DCE = ∠BCE.
∵CE = CE,
∴△DCE≌△BCE(SAS),
∴∠CDP = ∠CBE.
∵DC//AB,
∴∠CDP = ∠APD,
∴∠APD = ∠CBE.
(1)20 120° 30°
提示:
∵四边形ABCD是菱形,
∴AB = BC = CD = AD = 5,
$∠DAB + ∠ADC = 180°$,$∠DCA=\frac{1}{2}∠DCB=\frac{1}{2}∠DAB$,
∴菱形ABCD的周长为$4×5 = 20$,$∠ADC = 120°$,$∠DCA = 30°$.
(2)证明
∵四边形ABCD是菱形,
∴DC//AB,DC = BC,∠DCE = ∠BCE.
∵CE = CE,
∴△DCE≌△BCE(SAS),
∴∠CDP = ∠CBE.
∵DC//AB,
∴∠CDP = ∠APD,
∴∠APD = ∠CBE.
查看更多完整答案,请扫码查看


