《2025年少年班八年级数学下册浙教版》

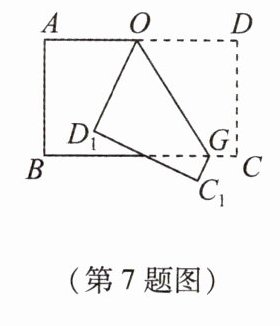
7 [2024·浙江丽水期中]将长方形纸条ABCD按如图的方式折叠，折痕为OG，点D落到点D1处，点C落到点C1处. 若∠OGB = 55°，则∠AOD1 = _______.

答案： 7.70°　解析：在长方形ABCD中，AD//BC，则∠DOG=∠OGB=55°.根据折叠的性质知∠D₁OG = ∠DOG = 55°，所以∠AOD₁ = 180° - 2∠DOG = 180° - 110° = 70°.

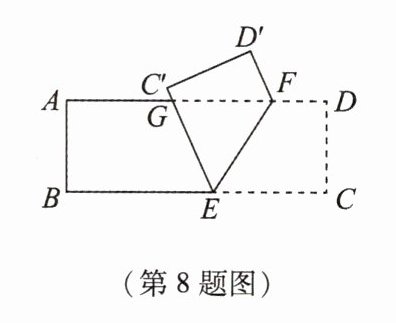
8 [2023·浙江金华校级月考]如图，把一张长方形纸片ABCD沿EF折叠后，点C，D分别落在C'，D'的位置，EC'交AD于点G. 已知∠EFG = 58°，那么∠BEG = _______.

答案： 8.64°　解析：
∵四边形ABCD为矩形，
∴AD//BC,
∴∠CEF=∠EFG=58°.由折叠的性质，得∠GEF=∠CEF=58°,
∴∠BEG=180°−∠GEF−∠CEF=64°.

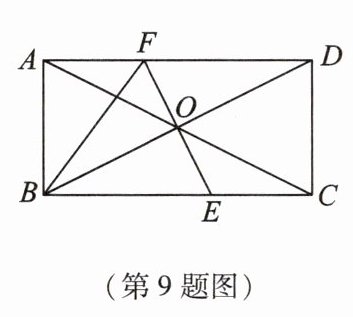
9 如图，矩形ABCD的周长为24 cm，两条对角线相交于点O，过点O作BD的垂线EF，分别交BC，AD于点E，F，连接BF，且AF = 3 cm，则矩形ABCD的面积为 （ ）


A. 24 cm²
B. 28 cm²
C. 32 cm²
D. 36 cm²

答案： 9.C　解析：
∵四边形ABCD为矩形，
∴OB=OD,∠BAF=90°.
∵EF⊥BD,
∴EF为线段BD的垂直平分线,
∴BF=DF;
∵矩形ABCD的周长为24cm，
∴AB+AD=12cm.设BF=DF=xcm,则AB=12−AD=12−AF−DF=(9−x)cm.在Rt△BAF中,
∵AB²+AF²=BF²,
∴(9−x)²+3²=x²,解得x=5,
∴AB=9−x=9−5=4(cm),AD=3+x=3+5=8(cm),
∴矩形ABCD的面积为4×8=32(cm²).故选C.

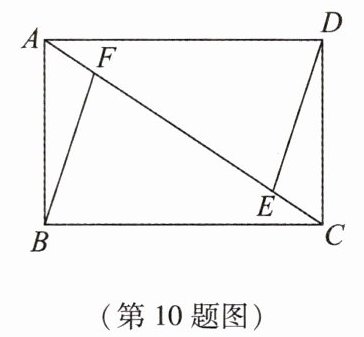
10 链教材 教材P115作业题第6题改编 [2024·浙江杭州期中]如图，在矩形ABCD中，点E，F为对角线AC上的两点，AE = AD，AF = CE，连接DE，BF. 若∠CAD = 40°，则∠BFE的度数为 （ ）


A. 75°
B. 70°
C. 55°
D. 40°

答案： 10.B　解析：
∵AE=AF+EF,AF=CE,
∴CF=CE+EF=AF+EF=AE.
∵四边形ABCD是矩形，
∴AD=BC,AD//BC.
∵AE=AD,
∴CF=BC,
∴∠CFB=∠CBF.
∵∠CAD=40°,AD//BC,
∴∠CAD=∠FCB=40°,
∴∠CFB=∠CBF=$\frac{1}{2}$(180°−∠FCB)=$\frac{1}{2}$(180°−40°)=70°.故选B.

11 如图，在矩形ABCD中，AD = 16，AB = 6，E为AD边的中点，点F从点B出发，以每秒1个单位长度的速度沿着边BC向终点C运动，连接AF，FE，EC. 设点F运动的时间为t秒.
（1）当t为何值时，AF = CE?
（2）是否存在某一时刻，使∠FEC = ∠DEC? 如果存在，求出t的值；如果不存在，请说明理由.

答案： 11.解：
(1)
∵四边形ABCD是矩形，
∴CD=AB=6,∠B=∠D=90°.
∵E为AD边的中点，
∴DE=$\frac{1}{2}$AD=$\frac{1}{2}$×16=8.在Rt△CDE中,由勾股定理,得CE=$\sqrt{DE^{2}+CD^{2}}$=$\sqrt{8^{2}+6^{2}}$=10.在Rt△ABF中,BF=t,AB=6,由勾股定理,得AF=$\sqrt{36 + t^{2}}$.
∵AF=CE,
∴$\sqrt{36 + t^{2}}$=10.解得t=8或t=−8(不符合题意，舍去),即当t=8时,AF=CE.
(2)存在.
∵四边形ABCD是矩形，
∴AD//BC,BC=AD=16,
∴∠DEC=∠ECF.
∵∠FEC=∠DEC,
∴∠FEC=∠ECF,
∴FE=FC.
∵BF=t,
∴FC=16−t.
∴(8−t)²+6²=(16−t)²,解得t=9.75.故存在t使∠FEC=∠DEC,此时t=9.75.