《2025年少年班八年级数学下册浙教版》

2 [2024·浙江杭州期中]如图(1)，在等腰三角形ABC中，AB = AC，点D是BC边上的动点，连接AD，将△ADC绕点A旋转至△AEB，使点C与点B重合，连接DE交AB于点F.
　　
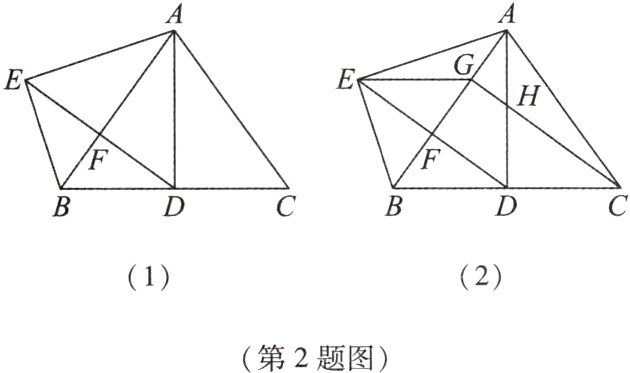
(1)若∠BAC = 80°，求∠ABE的大小.
(2)如图(2)，作EG//BC交AB于点G，连接CG交AD于点H.
①求证：四边形CDEG是平行四边形.
②若∠EGC - ∠CAD = 100°，求∠CAD的度数.

答案：
(1)解：
∵AB=AC，∠BAC=80°，
∴$\angle C=\frac{180 - 80^{\circ}}{2}=50^{\circ}$.
由题意，得△ADC≌△AEB，
∴∠ABE=∠C=50°.
(2)①证明：
∵△ADC≌△AEB，
∴∠ACB=∠ABE，EB=DC.
∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABC=∠ABE.
∵EG//BC，
∴∠EGB=∠GBC，
∴∠EGB=∠EBG，
∴EG=BE，
∴EG=DC.
∴四边形CDEG是平行四边形.
②解：
∵四边形CDEG是平行四边形，
∴∠EGC=∠EDC.
∵△ADC≌△AEB，
∴AE=AD，∠EAB=∠CAD.
∵∠EAB+∠BAD=∠CAD+∠BAD，
∴∠EAD=∠BAC.
∵AB=AC，AD=AE，
∴$\angle ACD=\frac{180^{\circ}-\angle BAC}{2}$，$\angle ADE=\frac{180^{\circ}-\angle EAD}{2}$，
∴∠ADE=∠ACD，
∴∠EDC = ∠ADE + ∠ADC = ∠ADE + (180° - ∠CAD - ∠ACD)=180° - ∠CAD.
∵∠EGC - ∠CAD=100°，
∴∠EDC=100°+∠CAD=180° - ∠CAD，
∴∠CAD=40°.

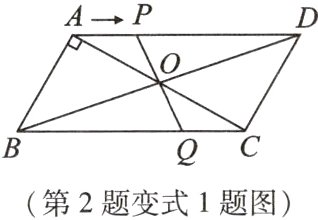
【变式1】如图，□ABCD的对角线AC，BD相交于点O，AB⊥AC，BC = 5，点P从点A出发，沿AD以每秒1个单位长度的速度向终点D运动. 连接PO并延长交BC于点Q. 设点P的运动时间为t秒.
(1)求BQ的长. (用含t的代数式表示)
(2)当四边形ABQP是平行四边形时，求t的值.
　　　　　　　　　　

答案： 解：
(1)
∵四边形ABCD是平行四边形，
∴OA=OC，AD//BC，
∴∠PAO=∠QCO.
∵∠AOP=∠COQ，
∴△APO≌△CQO，
∴CQ=AP=t.
∵BC=5，
∴BQ=5 - t.
(2)
∵AP//BQ，
∴当AP=BQ时，四边形ABQP是平行四边形，即t=5 - t，
∴$t=\frac{5}{2}$，
∴当四边形ABQP是平行四边形时，t的值为$\frac{5}{2}$.

【变式2】[2024·浙江杭州萧山月考]如图，在□ABCD中，点O是对角线AC的中点. 某数学学习小组要在AC上找两点E，F，使四边形BEDF为平行四边形，现总结出甲、乙两种方案如下：
　　　甲方案　　　　　　　　乙方案
　　　　O　　　　　　　　　　O
分别取AO，CO的中点E，F　作BE⊥AC于点E，DF⊥AC于点F
请回答下列问题：
(1)以上方案是否能得到四边形BEDF为平行四边形？若能，请证明；若不能，请说明理由.
(2)若EF = 2AE，S△AED = 6，求□ABCD的面积.

答案： 解：
(1)若选择甲方案：
如答图，连接BD.
∵在▱ABCD中，点O是对角线AC的中点，
∴AO=CO，BO=DO.
∵E，F分别为AO，CO的中点，
∴EO=FO，
∴四边形BEDF为平行四边形.
若选择乙方案：
∵四边形ABCD是平行四边形，
∴AD=BC，AD//CB，
∴∠EAD=∠FCB.
∵BE⊥AC，DF⊥AC，
∴BE//DF，∠BEF=∠AFD=90°.
∵在△ADF和△CBE中，$\begin{cases} \angle AFD=\angle CEB \\ \angle DAF=\angle BCE \\ AD = CB \end{cases}$，
∴△ADF≌△CBE(AAS)，
∴BE=DF.
又
∵BE//DF，
∴四边形BEDF为平行四边形.
(2)
∵四边形ABCD和四边形BEDF都为平行四边形，
∴AO=CO，EO=FO，
∴AE=CF.
∵EF=2AE，
∴EF=2FC，
∴AF=CE=3AE，AC=4AE.
∵$S_{\triangle AED}=6$，
∴$S_{\triangle ADC}=4S_{\triangle AED}=24$，
∴$S_{▱ABCD}=2S_{\triangle ADC}=48$.