《2025年少年班八年级数学下册浙教版》

1 [2023·浙江杭州期末]下列几何图形是中心对称图形的为 （ ）

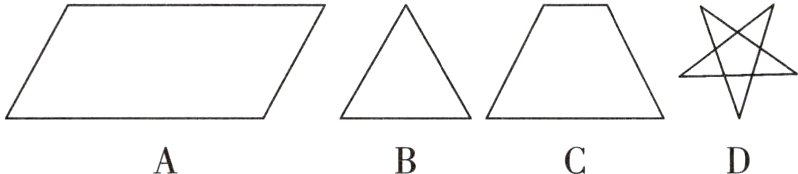
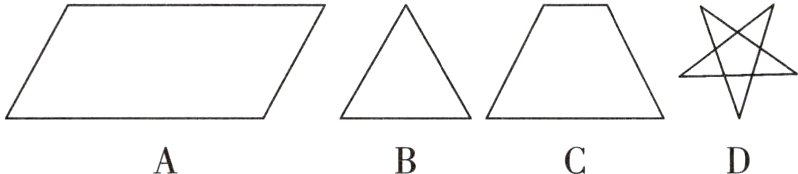
答案： A

2 真情境 关注奥运会 [2024·浙江温州月考]下列2024年巴黎奥运会的运动图标中,不是中心对称图形的是 （ ）

答案： B

3 [2023·浙江丽水期中]如图,将①②③④中的一块涂成阴影后能与图中原有阴影部分组成中心对称图形的是 （ ）

A.① B.② C.③ D.④

答案： C

4 如图的两个三角形（B,F,C,E四点共线）成中心对称,则对称中心是 （ ）


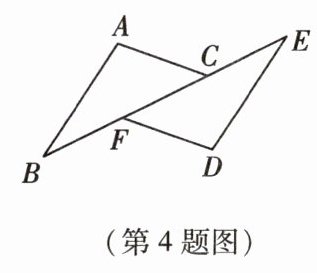
A.点C
B.点D
C.线段BC的中点
D.线段FC的中点

答案： D

5 如图,△ABC与△A'B'C'关于点O成中心对称,下列结论中不成立的是 （ ）


A.OB=OB'
B.∠ACB=∠A'B'C'
C.点A的对称点是点A'
D.BC//B'C'

答案： B 解析：
∵△ABC与△A′B′C′关于点O成中心对称，
∴OB=OB′，∠ACB=∠A′C′B′，点A的对称点是点A′，BC//B′C′，
∴选项B的结论不成立. 故选B.

6 如图,BO是等腰三角形ABC的底边的中线,AC = 2,BO = $\sqrt{15}$,△PQC与△BOC关于点C成中心对称,连接AP,则AP的长是 （ ）

A.4 B.4$\sqrt{2}$ C.3$\sqrt{5}$ D.2$\sqrt{6}$

答案： D 解析：
∵BO是等腰三角形ABC的底边的中线，AC = 2，
∴AO = CO = 1，BO⊥AC.
∵△PQC与△BOC关于点C成中心对称，BO = $\sqrt{15}$，
∴CQ = CO = 1，∠Q = ∠BOC = 90°，PQ = BO = $\sqrt{15}$，
∴AQ = AO + CO + CQ = 3，
∴AP = $\sqrt{AQ^{2}+PQ^{2}}$ = $\sqrt{3^{2}+(\sqrt{15})^{2}}$ = 2$\sqrt{6}$. 故选D.

7 链教材P92作业题第3题改编 [2023·浙江舟山期中]如图.（1）请你在图中画出△A'B'C',使其与△ABC关于点O成中心对称;
（2）新题型 开放性试题 请你在图中△ABC的边上找一个点并作出△DEF,使其与△ABC关于该点成中心对称,且△DEF与△ABC合成的图形为平行四边形.

答案：
解：
(1)如答图
(1)，△A′B′C′即为所求.
　　　
(2)如答图
(2)，点M，△DEF即为所求. (答案不唯一)

8 链教材P92作业题第2题改编 点M(1, - 2)关于原点对称的点的坐标是 （ ）
A.(-1, - 2) B.(1,2)
C.(-1,2) D.(-2,1)

答案： C

9 [2024·浙江衢州期中]如图,在平面直角坐标系中,等边三角形ABC的顶点B,C的坐标分别为(1,2),(3,2),直线AB交y轴于点M.若△ABC与△A₁B₁C₁关于点M成中心对称,则点A₁的坐标为 （ ）

A.(-2,-2 - $\sqrt{3}$) B.(-2,-2 - $\sqrt{3}$)
C.(-2,2 - 3$\sqrt{3}$) D.(-2,3$\sqrt{3}$ - 2)

答案：
C 解析：过点A作BC的垂线，垂足为N，如答图.
∵点B的坐标为(1，2)，点C的坐标为(3，2)，
∴BC//x轴，且BC = 3 - 1 = 2.
∵△ABC是等边三角形，
∴AB = BC = 2，BN = CN = 1，
∴AN = $\sqrt{2^{2}-1^{2}}$ = $\sqrt{3}$，
∴点A的坐标为(2，2 + $\sqrt{3}$). 设直线AB的表达式为y = kx + b，则$\begin{cases}k + b = 2\\2k + b = 2+\sqrt{3}\end{cases}$，解得$\begin{cases}k = \sqrt{3}\\b = -\sqrt{3}+2\end{cases}$，
∴直线AB的表达式为y = $\sqrt{3}x-\sqrt{3}+2$. 令x = 0，得y = -$\sqrt{3}+2$，
∴点M的坐标为(0，-$\sqrt{3}+2$).
∵△ABC与△A₁B₁C₁关于点M成中心对称，
∴点A和点A₁关于点M对称，
∴$\frac{2+x_{A_{1}}}{2}$ = 0，$\frac{2+\sqrt{3}+y_{A_{1}}}{2}$ = -$\sqrt{3}+2$，
∴x_{A_{1}} = - 2，y_{A_{1}} = - 3$\sqrt{3}+2$，
∴点A₁的坐标为(- 2，2 - 3$\sqrt{3}$). 故选C.