《2025年少年班八年级数学下册浙教版》

10. 若平行四边形的一边长是10 cm，则它的两条对角线的长可能是（ ）
A. 8 cm和12 cm
B. 8 cm和14 cm
C. 6 cm和10 cm
D. 6 cm和28 cm

答案： B

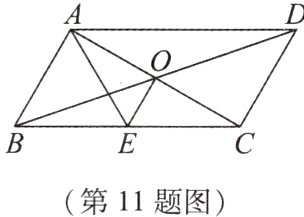
11. [2024·浙江宁波期中]如图，平行四边形ABCD的对角线AC，BD交于点O，AE平分∠BAD交BC于点E，且∠ADC = 60°，AB = $\frac{1}{2}$BC，连接OE.
下列结论：①∠ADO = 30°；②$S_{□ABCD}=AB\cdot AC$；③OB = AB；④$S_{四边形OECD}=\frac{3}{2}S_{\triangle AOD}$，其中成立的个数为（ ）


A. 1
B. 2
C. 3
D. 4

答案： B　解析：
∵四边形ABCD为平行四边形，∠ADC = 60°，
∴OA = OC，OB = OD，∠ABC = 60°，∠BAD = 120°.
∵AE平分∠BAD，
∴∠BAE = ∠DAE = 60°，
∴△ABE是等边三角形，
∴AB = AE = BE，∠AEB = 60°.
∵$AB=\frac{1}{2}BC$，
∴$BE=\frac{1}{2}BC$，
∴CE = BE = AE，
∴∠ACE = ∠CAE = 30°，
∴∠OAB = 90°，∠OAD = 30°.
∴在Rt△AOB中，OB＞OA，OB＞AB，则结论③不成立.
∴OD＞OA，
∴∠ADO≠∠OAD，即∠ADO≠30°，则结论①不成立.
∵∠OAB = 90°，即AB⊥AC，
∴$S_{□ABCD}=AB\cdot AC$，则结论②成立. 设平行四边形ABCD的面积为8a(a＞0)，则$S_{\triangle AOD}=S_{\triangle COD}=S_{\triangle BOC}=\frac{1}{4}S_{□ABCD}=2a$.
∵BE = CE，
∴$S_{\triangle BOE}=S_{\triangle COE}=\frac{1}{2}S_{\triangle BOC}=a$，
∴$S_{四边形OECD}=S_{\triangle COE}+S_{\triangle COD}=3a=\frac{3}{2}S_{\triangle AOD}$，则结论④成立. 综上，成立的个数为2. 故选B.

12. [2024·浙江杭州期中]如图，在平行四边形ABCD中，∠ABC = 135°，AD = 4$\sqrt{2}$，AB = 8，作对角线AC的垂直平分线EF，分别交对边AB，CD于点E和点F，则AE的长为_______.

答案：
$\frac{20}{3}$　解析：如答图，连接CE，过点C作CH⊥AB交AB的延长线于点H. 在平行四边形ABCD中，∠ABC = 135°，AD = $4\sqrt{2}$，
∴∠CBH = 45°，BC = $4\sqrt{2}$.
∵∠H = 90°，
∴∠BCH = 45°. 在Rt△BCH中，由勾股定理可得CH = BH = 4. 设AE = x，则BE = 8 - x.
∵EF垂直平分AC，
∴CE = AE = x.
∵在Rt△CEH中，$CH^{2}+EH^{2}=EC^{2}$，
∴$4^{2}+(8 - x + 4)^{2}=x^{2}$，解得$x=\frac{20}{3}$.

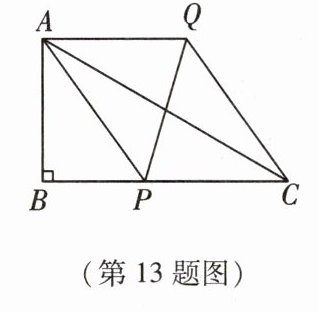
13. [2023·浙江温州期中]如图，在Rt△ABC中，∠B = 90°，∠ACB = 30°，BC = 3. P为BC边上任意一点，连接PA，以PA，PC为邻边作□PAQC，连接PQ，则PQ长的最小值为_______.

答案：

$\sqrt{3}$　解析：
∵∠B = 90°，∠ACB = 30°，BC = 3，
∴AC = 2AB，BC = $\sqrt{(2AB)^{2}-AB^{2}}=\sqrt{3}AB$，
∴AB = $\sqrt{3}$，AC = $2\sqrt{3}$. 如答图，设AC，PQ交于点O，过点O作OD⊥BC于点D.
∵四边形APCQ是平行四边形，
∴PO = QO，CO = $AO=\frac{1}{2}AC=\sqrt{3}$.
∵PQ最短也就是PO最短，即当P与D重合时，OP的值最小，
∴PQ长的最小值为2OD = 2×$\frac{1}{2}OC=\sqrt{3}$.

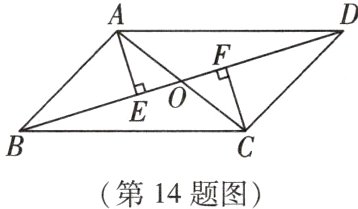
14. 链教材P88作业题第3题改编 如图，在□ABCD中，对角线AC，BD相交于点O，分别过点A，C作AE⊥BD，CF⊥BD，垂足分别为E，F.
（1）求证：AE = CF.
（2）若AC平分∠DAE，求证：CA平分∠BCF.

答案： 证明：
(1)
∵四边形ABCD是平行四边形，
∴AO = CO.
∵AE⊥BD，CF⊥BD，
∴∠AEO = ∠CFO = 90°. 在△AEO和△CFO中，$\begin{cases}∠AEO = ∠CFO\\∠EOA = ∠FOC\\AO = CO\end{cases}$，
∴△AEO≌△CFO(AAS)，
∴AE = CF.
(2)由
(1)，得∠EAO = ∠FCO. 又
∵AD//BC，
∴∠DAC = ∠BCA.
∵AC平分∠DAE，
∴∠EAO = ∠DAC，
∴∠FCO = ∠BCA，即CA平分∠BCF.

15. [2024·浙江绍兴期中]如图，平行四边形ABCD的对角线AC，BD交于点O，AE平分∠BAD，交BC于点E，且∠ADC = 60°.
（1）求证：AB = AE.
（2）若$\frac{AB}{BC}=m(0＜m＜1)$，AC = 4$\sqrt{3}$，连接OE.
①若$m=\frac{1}{2}$，求平行四边形ABCD的面积；
②设$\frac{S_{四边形OECD}}{S_{\triangle AOD}}=k$，试求k与m满足的关系.

答案：
(1)证明：
∵四边形ABCD是平行四边形，
∴∠ABC = ∠ADC = 60°，∠BAD = 120°.
∵AE平分∠BAD，
∴∠BAE = ∠EAD = 60°，
∴△ABE是等边三角形，
∴AB = AE.
(2)解：①
∵$\frac{AB}{BC}=m=\frac{1}{2}$，
∴$AB=\frac{1}{2}BC$，
∴$AE = BE=\frac{1}{2}BC$，
∴AE = CE.
∴∠ACB = ∠CAE = 30°，
∴∠BAC = 90°. 当AC = $4\sqrt{3}$时，由勾股定理，得AB = 4，
∴平行四边形ABCD的面积 = $2S_{\triangle ABC}=2\times\frac{1}{2}AB\cdot AC = 4\times4\sqrt{3}=16\sqrt{3}$.
②
∵四边形ABCD是平行四边形，
∴$S_{\triangle AOD}=S_{\triangle BOC}=\frac{1}{2}S_{\triangle BCD}$.
∵△ABE是等边三角形，
∴BE = AB = mBC. 设BC边上的高为h，BC的长为b，
∴$S_{\triangle BCD}=\frac{1}{2}bh$，$S_{\triangle OBE}=\frac{1}{2}\times\frac{h}{2}\times mb=\frac{mbh}{4}$，
∴$S_{四边形OECD}=S_{\triangle BCD}-S_{\triangle OBE}=\frac{bh}{2}-\frac{mbh}{4}=\frac{2 - m}{4}bh$.
∵$S_{\triangle AOD}=\frac{1}{2}\times\frac{h}{2}\times b=\frac{bh}{4}$，
∴$\frac{S_{四边形OECD}}{S_{\triangle AOD}}=\frac{\frac{2 - m}{4}bh}{\frac{bh}{4}}=k$，
∴2 - m = k，
∴m + k = 2.