《2025年启东中学作业本七年级数学下册人教版》

1. 如图，在平面直角坐标系xOy中，动点P按图中箭头所示方向依次运动，第1次从点(－1,0)运动到点(0,1)，第2次运动到点(1,0)，第3次运动到点(2,－2)……按这样的运动规律，动点P第2024次运动到点（ ）

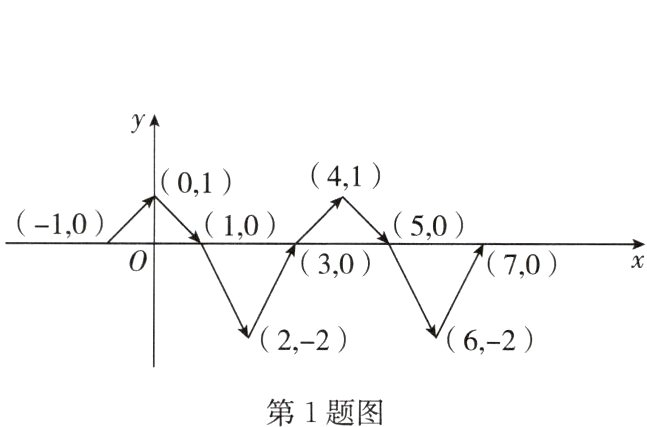
A. (2022,－2)
B. (2023,0)
C. (2024,1)
D. (2023,－2)

答案： B

2. 如图，在平面直角坐标系中，长方形ABCD的四个顶点的坐标分别为A(－1,2)，B(－1,－1)，C(1,－1)，D(1,2)，点P从点A出发，沿长方形的边顺时针运动，速度为2个单位长度/秒，点Q从点A出发，沿长方形的边逆时针运动，速度为3个单位长度/秒，记点P，Q在长方形边上第1次相遇时的点为M1，第二次相遇时的点为M2，第三次相遇时的点为M3……则点M2024的坐标为（ ）

A. (1,0)
B. (1,2)
C. (0,－1)
D. (－1,0)

答案： C

3. (2023·西城区月考)如图，在平面直角坐标系中有个点P(1,0)，点P第1次向上跳动1个单位长度至点P1(1,1)，紧接着第2次向左跳动2个单位长度至点P2(－1,1)，第3次向上跳动1个单位长度，第4次向右跳动3个单位长度，第5次向上跳动1个单位长度，第6次向左跳动4个单位长度……依此规律跳动下去，点P7的坐标是________，点P第2024次跳动至点P2024，点P2024的坐标是________.

答案： (-2,4)　(507,1012)

4. 在平面直角坐标系中，一只蚂蚁从原点O出发，按向上、向左、向下、向下、向左、向上的方向依次不断移动得A1，A2，A3，A4，A5，A6，…，每次移动的距离分别为1,1,1,2,2,2,3,3,3，…，其行走路线如图所示.
(1)写出下列各点的坐标：A3，A6，A9，A12；
(2)写出点A3n的坐标(n为正整数)；
(3)求蚂蚁从原点O移动到点A33的路程.

答案： 解:
(1)A₃(-1,0),A₆(-3,0),A₉(-6,0),A₁₂(-10,0).
(2)点A₃ₙ的坐标为(-$\frac{n^{2}+n}{2}$,0).
(3)
∵33÷3=11,
∴蚂蚁从原点O移动到点A₃₃的路程为(1+1+1)+(2+2+2)+…+(11+11+11)=3×(1+2+3+...+11)=3×66=198.