《2025年启东中学作业本七年级数学下册人教版》

10.下列说法正确的是（ ）
A.若ab＝0，则点P(a,b)表示原点
B.点(1,－a²)一定在第四象限
C.已知点A(1,－3)，B(1,3)，则直线AB平行于y轴
D.已知点A(1,－3)，AB//y轴，且AB＝4，则点B的坐标为(1,1)

答案： C

11.(2024春·漳平期末)若点P(m＋5,m－3)在第二、四象限的角平分线上，则m＝________.

答案： -1

12.(2024春·鼓楼区月考)在平面直角坐标系中，点P(－2,－3)到y轴的距离为________.

答案： 2

13.(2024·宿迁)点P(a²＋1,－3)在第________象限.

答案： 四

14.已知平面直角坐标系内两点M(5,a)，N(b,－2).
(1)若直线MN//x轴，则a________，b________；
(2)若直线MN//y轴，则a________，b________；
(3)若直线MN为第一、三象限的角平分线，则a________，b________；
(4)若直线MN为第二、四象限的角平分线，则a________，b________.

答案：
(1)=-2 ≠5
(2)≠-2 =5
(3)=5 =-2
(4)=-5 =2

15.在平面直角坐标系中，已知点P(2m＋4,m－1).
(1)①若点P在y轴上，则点P的坐标为________；
②若点P的纵坐标比横坐标大3，则点P的坐标为________.
(2)点P________是坐标原点.(填“可能”或“不可能”)

答案：
(1)①(0,-3) ②(-12,-9)
(2)不可能

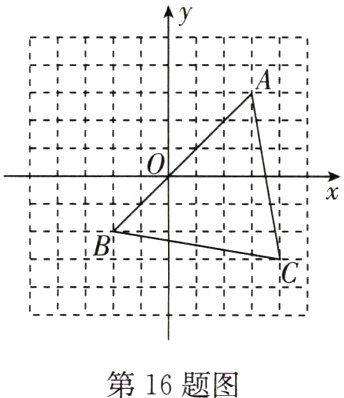
16.在如图所示的正方形网格中，每个小正方形的边长均为1，三角形ABC的三个顶点恰好是正方形网格的格点.
(1)写出图中所示三角形ABC各顶点的坐标；
(2)求出此三角形的面积.

答案：
解：
(1)A(3,3),B(-2,-2),C(4,-3).
(2)如答图.

$S_{\triangle ABC}=S_{正方形DECF}-S_{\triangle BEC}-S_{\triangle ADB}-S_{\triangle AFC}=6×6 - \frac{1}{2}×6×1 - \frac{1}{2}×5×5 - \frac{1}{2}×6×1=\frac{35}{2}.$

17.如图，已知点A(－4,0)，B(6,0)，C(2,4)，D(－3,2).
(1)求四边形ABCD的面积；
(2)求三角形BCD的面积；
(3)在y轴上找一点P，使三角形APB的面积等于四边形ABCD面积的一半，求点P的坐标.

答案：
解：
(1)如答图,作 DE⊥x 轴于点 E,CF⊥x 轴于点 F.

∵A(-4,0),B(6,0),C(2,4),D(-3,2),
∴AE=1,EF=5,BF=4,AB=10,DE=2,CF=4,
∴$S_{四边形ABCD}=S_{\triangle ADE}+S_{四边形CDEF}+S_{\triangle BCF}=\frac{1}{2}×1×2+\frac{1}{2}×(2 + 4)×5+\frac{1}{2}×4×4=24$.
(2)$S_{\triangle BCD}=S_{四边形ABCD}-S_{\triangle ABD}=24 - \frac{1}{2}×10×2=14$.
(3)
∵$S_{\triangle APB}=\frac{1}{2}×AB×OP=\frac{1}{2}×24$,
∴OP=2.4,
∴点 P 的坐标为(0,2.4)或(0,-2.4).