《2025年启东中学作业本七年级数学下册人教版》

11.(8分)求下列各式中$x$的值.
　(1)$x^{2}-3 = 0$; (2)$(2x - 1)^{2}-169 = 0$; (3)$(3x - 1)^{3}-125 = 0$.

答案：
(1)$x=\pm\sqrt{3}$
(2)$x=7$或$x=-6$
(3)$x=2$

12.(8分)已知实数$a + 9$的平方根是±5,$2b - a$的立方根是－2,求式子$\sqrt{a}-\sqrt{b}$的值.

答案： 解：$\because$实数$a + 9$的平方根是$\pm5$，$2b - a$的立方根是$-2$，
$\therefore a + 9=25$，$2b - a=-8$，解得$a=16$，$b=4$.
$\therefore\sqrt{a}-\sqrt{b}=\sqrt{16}-\sqrt{4}=4 - 2=2$.

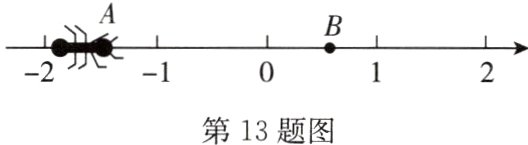
13.(8分)如图,点$A$表示的数为－$\sqrt{2}$,一只蚂蚁从点$A$沿数轴向右爬2个单位长度后到达点$B$,设点$B$表示的数为$n$.
　(1)求$n$的值;
　(2)求$\vert n + 1\vert+(n + 2\sqrt{2}-2)$的值.
　　　

答案： 解：
(1)$\because$蚂蚁从点$A$沿数轴向右爬$2$个单位长度到达点$B$，
$\therefore$点$B$表示的数比点$A$表示的数大$2$.
$\because$点$A$表示的数为$-\sqrt{2}$，点$B$表示的数为$n$，
$\therefore n=-\sqrt{2}+2$.
(2)$|n + 1|+(n + 2\sqrt{2}-2)$
$=|-\sqrt{2}+2+1|+(-\sqrt{2}+2+2\sqrt{2}-2)$
$=3-\sqrt{2}+\sqrt{2}=3$.

14.(10分)(2023·弋江区期末)某小区有一块面积为$196m^{2}$的正方形空地,开发商计划在此空地上建一个面积为$100m^{2}$的长方形花坛(长方形花坛的边与正方形空地的边平行),使长方形的长是宽的2倍.请你通过计算说明开发商能否实现这个愿望.(参考数据:$\sqrt{2}\approx1.414$,$\sqrt{50}\approx7.071$)

答案： 解：设长方形花坛的宽为$x$m，则长为$2x$m.
由题意得$2x\cdot x=100$，$\therefore x^{2}=50$.
$\because x＞0$，
$\therefore x=\sqrt{50}$，$2x=2\sqrt{50}$.
$\because$正方形空地的面积为$196$m²，
$\therefore$正方形空地的边长为$14$m.
$\because 2\sqrt{50}＞14$，
$\therefore$开发商不能实现这个愿望.

15.(10分)我们知道$a + b = 0$时,$a^{3}+b^{3}=0$也成立,若将$a$看成$a^{3}$的立方根,$b$看成$b^{3}$的立方根,我们能否得出这样的结论:若两个数的立方根互为相反数,则这两个数也互为相反数?
　(1)试举一个例子来判断上述猜测结论是否成立;
　(2)若$\sqrt[3]{\frac{2x - 1}{7}}$与$\sqrt[3]{-\frac{x - 9}{4}-3}$互为相反数,求$4-\sqrt{x}$的值.

答案： 解：
(1)$2+(-2)=0$，$2^{3}=8$，$(-2)^{3}=-8$，$8+(-8)=0$，
因此结论成立.(举例不唯一)
(2)由
(1)验证的结果可得$\frac{2x - 1}{7}-\frac{x - 9}{4}-3=0$，
去分母，得$4(2x - 1)-7(x - 9)-84=0$，
去括号、移项、合并同类项，得$x=25$.
故$4-\sqrt{x}=4 - 5=-1$.