《2025年学习与评价八年级数学下册江苏凤凰教育出版社》

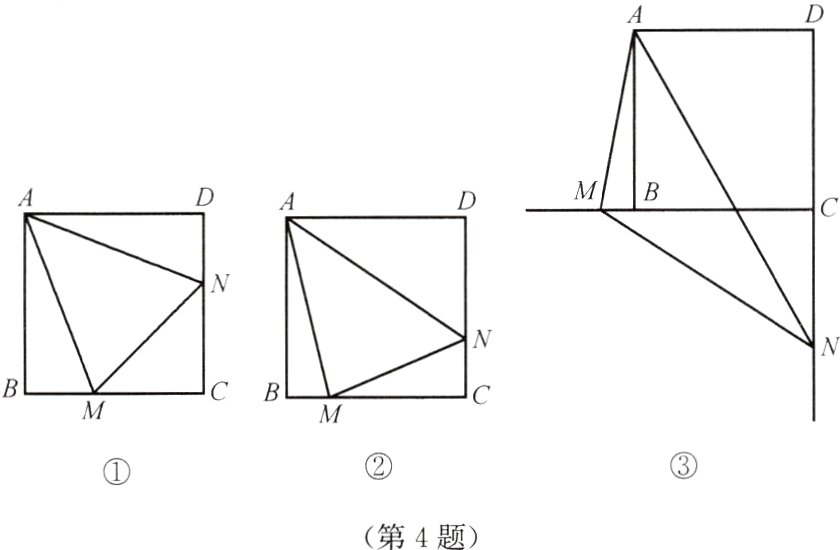
4. 如图，在正方形ABCD中，∠MAN = 45°，∠MAN绕点A按顺时针方向旋转，它的两边分别交CB、DC(或它们的延长线)于点M、N. 当∠MAN绕点A旋转到BM = DN时(图①)，易证BM + DN = MN.
(1) 当∠MAN绕点A旋转到BM≠DN时(图②)，关于线段BM、DN与MN之间的数量关系，你有什么发现? 写出你发现的结论，并证明.
(2) 当∠MAN绕点A旋转到如图③的位置时，关于线段BM、DN与MN之间的数量关系，你有什么发现? 请直接写出你的发现.
　　　　　　　　　

答案：

5. 封闭的中心对称图形都可以过对称中心作一条直线把它分成面积相等的两部分. 例如，经过圆心的直线把圆分成面积相等的两部分(图①).
　　　　　　
请在图②、图③中分别画一条直线把它们分成面积相等的两部分，其中图②中的四边形ABCD是平行四边形，图③中的∠A = ∠B = ∠C = ∠D = ∠E = ∠EFD = 90°.

答案：