《2025年顶尖课课练九年级数学下册华师大版》

16. 如果一个正整数能表示成两个连续偶数的平方差，那么称这个正整数为 “智慧数”．例如，$4 = 2^{2}-0^{2}$，$12 = 4^{2}-2^{2}$，$4$，$12$ 就是 “智慧数”．
（1）请再写出一个不是 “$4$” 和 “$12$” 的 “智慧数”，并说明理由；
（2）试说明所有的 “智慧数” 都是 $4$ 的倍数．

答案：
(1) 答案不唯一，如 20，因为 20 = 6² - 4²，所以 20 是“智慧数”
(2) 略

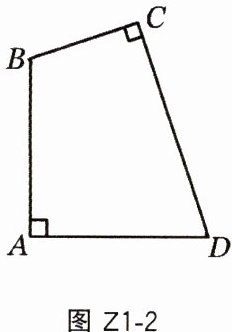
17. 如图 Z1-2，在四边形 $ABCD$ 中，$\angle DAB=\angle BCD = 90^{\circ}$，$AB = AD$，$BC + CD = m$．
（1）当 $BC\cdot CD = 8$，$m = 6$ 时，求 $AB$ 的长；
（2）求四边形 $ABCD$ 的面积（用含 $m$ 的代数式表示）．
图 Z1-2

答案：
(1) $\sqrt{10}$
(2) $\frac{1}{4}m^{2}$