《2025年顶尖课课练九年级数学下册华师大版》

4. 如图 26.3.2-3，在平面直角坐标系 $xOy$ 中，边长为 $2$ 的正方形 $OABC$ 的顶点 $A$、$C$ 分别在 $x$ 轴、$y$ 轴的正半轴上，二次函数 $y = -\frac{2}{3}x^{2}+bx + c$ 的图象经过 $B$、$C$ 两点.
(1) 求该二次函数的表达式；
(2) 结合函数的图象探索：当 $y＞0$ 时，$x$ 的取值范围.

答案： $y = -\frac{2}{3}x^{2}+\frac{4}{3}x + 2$@@$-1 ＜ x ＜ 3$

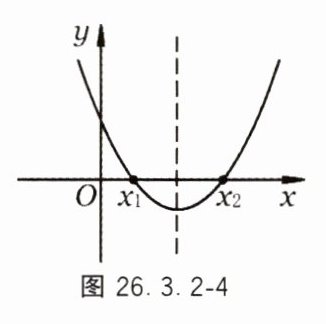
5. 已知函数 $y = x^{2}-2x + m$（$m$ 为常数）的图象如图 26.3.2-4 所示，如果当 $x = a$ 时，$y＜0$，那么当 $x = a - 2$ 时，函数值（ ）.


A. $y＜0$
B. $0＜y＜m$
C. $y = m$
D. $y＞m$

答案： D

6. 下面是博学小组研究性学习报告的部分内容，请认真阅读并完成相应任务.
“阶梯 $n$ 点”的研究总结
【一般概念】若抛物线 $C$ 上存在一点 $P$，点 $P$ 的横、纵坐标之和为 $n$，则称点 $P$ 为抛物线 $C$ 上的“阶梯 $n$ 点”.
例如：点 $P(0,1)$ 就叫做抛物线 $C$：$y = x^{2}+x + 1$ 的“阶梯 $1$ 点”.
【求抛物线 $C$ 上的“阶梯 $n$ 点”的方法】例如：求抛物线 $C$：$y = x^{2}+x + 1$ 上的“阶梯 $9$ 点”的点 $P$. 设点 $P$ 的坐标为 $(x,y)$.
$\because x + y = 9$，$\therefore y = 9 - x$. $\therefore 9 - x = x^{2}+x + 1$.
整理，得 $x^{2}+2x - 8 = 0$，解得 $x_{1}=2$，$x_{2}=-4$.
$\therefore$ 点 $P$ 的坐标为 $\underline{\text{▲}}$ 或 $(-4,13)$.
任务：
(1) 直接写出研究报告中“▲”处空缺的内容：__________；
(2) 按照材料中的方法，求抛物线 $C$：$y = x^{2}+2x + 3$ 上的“阶梯 $1$ 点” $P$；
(3) 若抛物线 $C$：$y = x^{2}+x + c$ 上存在“阶梯 $2$ 点” $P$，直接写出 $c$ 的取值范围.

答案： (2, 7)@@(-2, 3) 或 (-1, 2)@@$c\leq3$