第31页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
5. 某数学小组对数学学习中有关汽车的刹车距离有疑惑,于是他们走进汽车研发中心考察.
【知识背景】“道路千万条,安全第一条”,刹车后还要继续向前行驶一段距离才能停止,这段距离称为刹车距离.
【探究发现】汽车研发中心设计一款新型汽车,现在模拟汽车在高速公路上以某一速度行驶时,对它的刹车性能进行测试,数学小组收集、整理数据,并绘制函数图象.
发现:开始刹车后行驶的距离 $y$(单位:$\text{m}$)与刹车后行驶时间 $t$(单位:$\text{s}$)之间成二次函数关系,函数图象如图 26.3.1-4 所示.
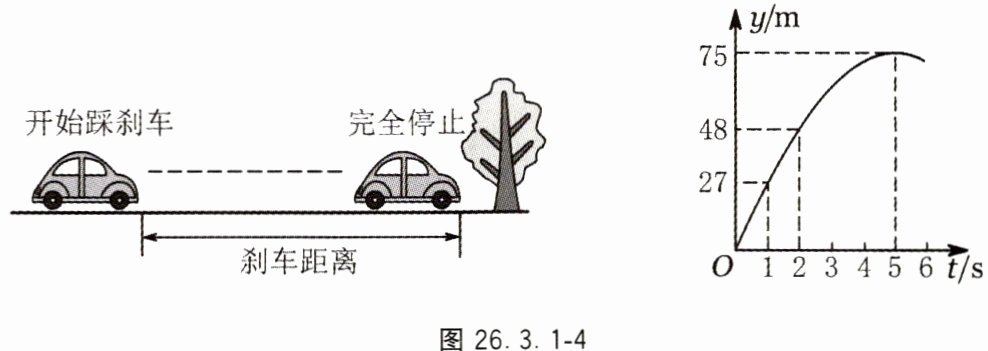
【问题解决】请根据以上信息,完成下列问题:
(1) 求二次函数的解析式(不要求写出自变量的取值范围);
(2) 若在汽车前 $60\ \text{m}$ 处,有一测速仪,问:当汽车刹车过程中,经过多少时间,汽车与测速仪相距 $12\ \text{m}$?
(3) 若汽车司机发现正前方 $80\ \text{m}$ 处有一辆抛锚的车停在路面,立刻刹车,问:该车在不变道的情况下是否会撞到抛锚的车?试说明理由.
【知识背景】“道路千万条,安全第一条”,刹车后还要继续向前行驶一段距离才能停止,这段距离称为刹车距离.
【探究发现】汽车研发中心设计一款新型汽车,现在模拟汽车在高速公路上以某一速度行驶时,对它的刹车性能进行测试,数学小组收集、整理数据,并绘制函数图象.
发现:开始刹车后行驶的距离 $y$(单位:$\text{m}$)与刹车后行驶时间 $t$(单位:$\text{s}$)之间成二次函数关系,函数图象如图 26.3.1-4 所示.

【问题解决】请根据以上信息,完成下列问题:
(1) 求二次函数的解析式(不要求写出自变量的取值范围);
(2) 若在汽车前 $60\ \text{m}$ 处,有一测速仪,问:当汽车刹车过程中,经过多少时间,汽车与测速仪相距 $12\ \text{m}$?
(3) 若汽车司机发现正前方 $80\ \text{m}$ 处有一辆抛锚的车停在路面,立刻刹车,问:该车在不变道的情况下是否会撞到抛锚的车?试说明理由.
答案:
$y = -3t^{2}+30t$@@2 s@@不会,理由略
查看更多完整答案,请扫码查看


