第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
6. 抛物线$y = - x^{2}+bx + c$上部分点的横坐标$x$、纵坐标$y$的对应值如下表所示:
|$x$|$\cdots$| - 2| - 1|0|1|2|$\cdots$|
|$y$|$\cdots$|0|4|6|6|4|$\cdots$|
从上表可知,下列说法中错误的是( ).
A. 抛物线与$x$轴的一个交点坐标为( - 2,0)
B. 抛物线与$y$轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线$x = 0$
D. 抛物线在对称轴左侧部分是上升的
|$x$|$\cdots$| - 2| - 1|0|1|2|$\cdots$|
|$y$|$\cdots$|0|4|6|6|4|$\cdots$|
从上表可知,下列说法中错误的是( ).
A. 抛物线与$x$轴的一个交点坐标为( - 2,0)
B. 抛物线与$y$轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线$x = 0$
D. 抛物线在对称轴左侧部分是上升的
答案:
C
7. 若不论$m$取任何实数,抛物线$y = x^{2}+4mx + 4m^{2}+m - 1$的顶点都在一条直线上,则这条直线的表达式是__________.
答案:
$y = -\frac{1}{2}x - 1$
8. 如图26.2.2 - 7,已知二次函数$y = a(x - h)^{2}+\sqrt{3}$的图象经过原点$O(0,0)$、$A(2,0)$.

(1)该函数图象的对称轴是____________;
(2)若将线段$OA$绕点$O$逆时针旋转$60^{\circ}$到$OA'$,请问:点$A'$是否为该函数图象的顶点?

(1)该函数图象的对称轴是____________;
(2)若将线段$OA$绕点$O$逆时针旋转$60^{\circ}$到$OA'$,请问:点$A'$是否为该函数图象的顶点?
答案:
(1)直线$x = 1$@@(2)是
9. 若二次函数$y = |a|x^{2}+bx + c$的图象经过点$A(m,n)$、$B(0,y_{1})$、$C(3 - m,n)$、$D(\sqrt{2},y_{2})$、$E(2,y_{3})$,则$y_{1}$、$y_{2}$、$y_{3}$的大小关系是( ).
A. $y_{1}<y_{2}<y_{3}$
B. $y_{1}<y_{3}<y_{2}$
C. $y_{3}<y_{2}<y_{1}$
D. $y_{2}<y_{3}<y_{1}$
A. $y_{1}<y_{2}<y_{3}$
B. $y_{1}<y_{3}<y_{2}$
C. $y_{3}<y_{2}<y_{1}$
D. $y_{2}<y_{3}<y_{1}$
答案:
D
10. 已知抛物线$y = ax^{2}+bx + c$的对称轴为直线$x = 1$,与$x$轴的一个交点坐标为( - 1,0),其部分函数图象如图26.2.2 - 8所示,给出下列结论:①$abc>0$;②$b^{2}-4ac>0$;③$3a + c = 0$;④方程$ax^{2}+bx + c = 0$的两个根是$x_{1} = - 1$,$x_{2} = 3$;⑤当$x<1$时,$y$随$x$的增大而减小. 其中结论正确的是____________.(填序号)
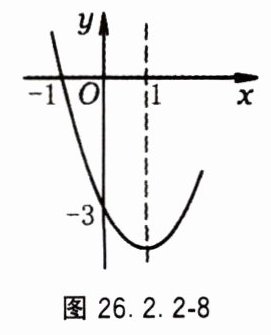

答案:
①②③④⑤
11. 已知函数$y=\begin{cases}-x^{2}-2x - 2, &x\leqslant - 1, \\x, & - 1<x\leqslant1, \\x^{2}-2x + 2, &x>1, \end{cases}$请利用探究函数图象的经验画出此函数的大致图象.
答案:
略
查看更多完整答案,请扫码查看


