《2025年黄冈小状元同步计算天天练六年级数学下册北师大版》

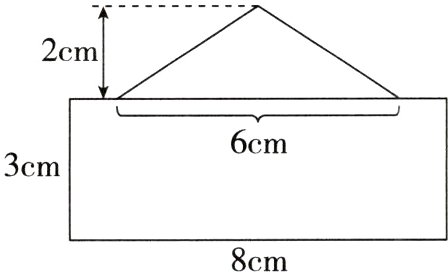
1. 一个圆锥与圆柱的底面圆心重合，从圆锥顶点处垂直底面切开，剖面图如下图，求原来组合图形的体积。
$V_{总}=V_{圆柱}+V_{圆锥}$
$=\pi(\underline{\quad\quad}\div2)^{2}\times\underline{\quad\quad}+\frac{1}{3}\times\pi(\underline{\quad\quad}\div2)^{2}\times\underline{\quad\quad}$
$=\pi\times\underline{\quad\quad}\times\underline{\quad\quad}+\frac{1}{3}\pi\times\underline{\quad\quad}\times\underline{\quad\quad}$
$=\underline{\quad\quad}\pi+\underline{\quad\quad}\pi$
$=\underline{\quad\quad}\pi$
$=\underline{\quad\quad}\times3.14$
$=\underline{\quad\quad}(\quad\quad)$

答案： $V_{总}=V_{圆柱}+V_{圆锥}$
　　　$=\pi\times(8\div2)^{2}\times3+\frac{1}{3}\times\pi\times(6\div2)^{2}\times2$
　　$=\pi\times16\times3+\frac{1}{3}\pi\times9\times2$
　　$=48\pi + 6\pi$
　　$=54\pi$
　　$=54\times3.14$
　　$=169.56(cm^{3})$

2. 沿圆柱的底面直径垂直底面把圆柱切开，剖面图如下图所示，$S_{剖}=40cm^{2}$。

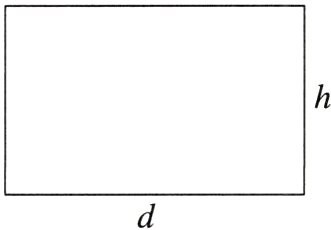
（1）求原来圆柱的侧面积。
$S_{剖}=dh=\underline{\quad\quad}(\quad\quad)$
$S_{侧}=C_{底}\times h$
$=\pi dh$
$=\pi\times\underline{\quad\quad}$
$=3.14\times\underline{\quad\quad}$
$=\underline{\quad\quad}(\quad\quad)$
（2）若$C_{底}=25.12cm$，求$V_{圆柱}$。
$d = C_{底}\div\pi$
$=\underline{\quad\quad}\div3.14$
$=\underline{\quad\quad}(\quad\quad)$
$h = S_{剖}\div d$
$=\underline{\quad\quad}\div\underline{\quad\quad}$
$=\underline{\quad\quad}(\quad\quad)$
$V_{圆柱}=\pi(d\div2)^{2}h$
$=$
$=$
$=$

答案：
(1) $S_{剖}=dh = 40(cm^{2})$
$S_{侧}=C_{底}\times h$
　　　$=\pi dh$
　　　$=\pi\times40$
　　　$=3.14\times40$
　　　$=125.6(cm^{2})$
(2) $d = C_{底}\div\pi$
　　$=25.12\div3.14$
　　$=8(cm)$
　$h = S_{剖}\div d$
　　$=40\div8$
　　$=5(cm)$
　$V_{圆柱}=\pi(d\div2)^{2}h$
　　　$=3.14\times(8\div2)^{2}\times5$
　　　$=3.14\times16\times5$
　　　$=251.2(cm^{3})$