《2025年通城学典课时作业本七年级数学下册人教版南通专版》

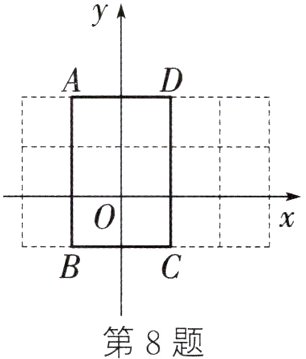
8. 如图，在平面直角坐标系中，长方形ABCD的四个顶点的坐标分别为A(-1,2)，B(-1,-1)，C(1,-1)，D(1,2)，点P从点A出发，沿长方形的边顺时针运动，速度为每秒2个单位长度，点Q从点A出发，沿长方形的边逆时针运动，速度为每秒3个单位长度，记点P，Q在长方形的边上第一次相遇时位于点$M_{1}$处，第二次相遇时位于点$M_{2}$处，第三次相遇时位于点$M_{3}$处……则点$M_{ 2 024}$的坐标为（ ）
A.（1,0） B.（-1,0） C.（1,2） D.（0,-1）
　　　　　　　　　　

答案： D 解析：长方形ABCD的周长为(3 + 2)×2 = 10. 设经过t秒点P,Q第一次相遇，则点P走的路程为2t，点Q走的路程为3t. 根据题意，得2t + 3t = 10，解得t = 2.
∴当t = 2时，点P，Q第一次相遇.
∴点M₁的坐标为(1,0). 当t = 4时，点P，Q第二次相遇.
∴点M₂的坐标为(-1,0). 当t = 6时，点P，Q第三次相遇.
∴点M₃的坐标为(1,2). 当t = 8时，点P，Q第四次相遇.
∴点M₄的坐标为(0,-1). 当t = 10时，点P，Q第五次相遇.
∴点M₅的坐标为(-1,2). 当t = 12时，点P，Q第六次相遇.
∴点M₆的坐标为(1,0).
∴五次相遇一循环.
∵2024÷5 = 404……4，
∴点M₂₀₂₄的坐标为(0,-1).

9. 若MN//x轴，点M的坐标是(-3,5)，线段MN的长为6，则点N的坐标是___________。

答案： (-9,5)或(3,5)

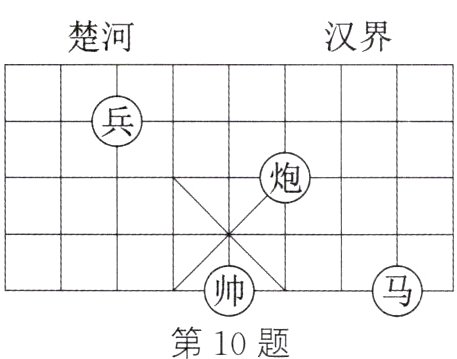
10.（教材P70习题9.1第5题变式）如图，请在象棋棋盘上建立平面直角坐标系，使“帅”所在点的坐标为(-1,-2)，则“马”所在点的坐标为_______。
　　　　　　

答案： (2,-2)

11.（教材P70习题9.1第9题变式）已知点A(-5,0)，B(3,0)，在y轴上有一点C满足三角形ABC的面积为16，那么点C的坐标为____________。

答案： (0,4)或(0,-4)

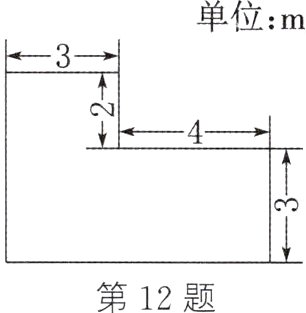
12. 小超设计的广告模板草图如图所示，小超想通过电话向小强描述该草图。假如你是小超，你如何利用刚学的平面直角坐标系知识把这个草图告诉小强呢？
　　　　

答案：
如图，建立平面直角坐标系(1个单位长度表示1 m)，标出点(0,0)，(0,5)，(3,5)，(3,3)，(7,3)，(7,0)，再把各点依次连接，所得图案即为小超设计的草图(答案不唯一)

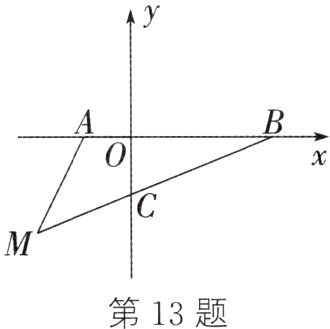
13. 如图，在平面直角坐标系中，点A(a,0)，B(b,0)，且a，b满足$\sqrt{a + 1}+(b - 3)^2 = 0$。
（1）a = ________，b = _______；
（2）若在第三象限内有一点M(-2,m)，用含m的式子表示三角形ABM的面积；
（3）在（2）的条件下，线段BM与y轴相交于点C(0,-$\frac{9}{10}$)，当m = -$\frac{3}{2}$时，P是y轴上的动点，当满足三角形PBM的面积是三角形ABM的面积的2倍时，求点P的坐标。
　　　　

答案：
(1) -1 3
(2)
∵a = -1，b = 3，
∴A(-1,0)，B(3,0).
∴AB = 4.
∵M(-2,m)，且点M在第三象限，
∴m ＜ 0.
∴三角形ABM的面积 = $\frac{1}{2}$×4×(-m) = -2m
(3) 当m = -$\frac{3}{2}$时，M(-2,-$\frac{3}{2}$)，S_{三角形ABM} = -2m = -2×(-$\frac{3}{2}$) = 3.
∵三角形PBM的面积是三角形ABM的面积的2倍，三角形PBM的面积 = 三角形MPC的面积 + 三角形BPC的面积，
∴$\frac{1}{2}$PC×2 + $\frac{1}{2}$PC×3 = 6，解得PC = $\frac{12}{5}$. 当点P在点C的下方时，P(0,-$\frac{9}{10}$ - $\frac{12}{5}$)，即P(0,-$\frac{33}{10}$)；当点P在点C的上方时，P(0,-$\frac{9}{10}$ + $\frac{12}{5}$)，即P(0,$\frac{3}{2}$). 综上所述，点P的坐标为(0,-$\frac{33}{10}$)或(0,$\frac{3}{2}$)