《2025年通城学典课时作业本七年级数学下册人教版南通专版》

8. 如图，从“输入$x$”到“结果是否小于18”为一次程序操作. 若输入$x$后程序操作仅一次就停止了，则$x$的取值范围是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(　　　)
A. $x \leq 8$　　　　　　　B. $x ＜ 8$　　　　　　　C. $x \geq 8$　　　　　　　D. $x ＞ 8$
　　　　 　　　　　

答案： B

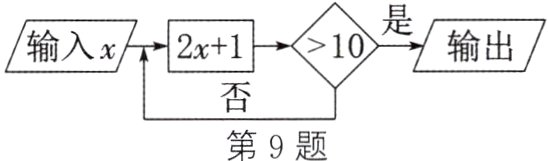
9. 按如图所示的程序计算，若开始输入$x$的值为正整数，规定程序运行到“判断结果是否大于10”为一次运算. 例如：当$x = 2$时，输出结果为11. 若经过两次运算就停止，则$x$可以取的所有值是________.

答案： 2或3或4

10. 对于实数$a$，$b$，规定$a\oplus b = a + b - ab$，则不等式$2\oplus(2x - 1) ＜ 1$的解集为________.

答案： $ x＞1 $

11. 对于三个数$a$，$b$，$c$，用$\max\{a,b,c\}$表示这三个数中的最大数，例如：$\max\{ - 3,-5,0\} = 0$，$\max\{ - 2,-1,a\} =\begin{cases}a(a \geq - 1),\\-1(a ＜ - 1).\end{cases}$若$\max\{2,6 - x,2x - 7\} = 2$，则$x$的取值范围是__________.

答案： $ 4\leqslant x\leqslant4.5 $

12. 我们把$\begin{vmatrix}a&b\\c&d\end{vmatrix}$称为二阶行列式，规定它的运算法则为$\begin{vmatrix}a&b\\c&d\end{vmatrix}=ad - bc$. 例如：$\begin{vmatrix}2&3\\4&5\end{vmatrix}=2\times5 - 3\times4 = - 2$.
　　(1)若$\begin{vmatrix}-1&2x - 1\\0.5&x\end{vmatrix}=0$，则$x =$________；若$\begin{vmatrix}2&1\\3 - x&x\end{vmatrix}＞0$，则$x$的取值范围是________.
　　(2)若正整数$m$，$n$满足$-2 ＜ \begin{vmatrix}1&n\\m&4\end{vmatrix}＜0$，求$m + n$的值.
　　(3)若非负数$x$，$y$满足$\begin{vmatrix}x - 1&y\\2&3\end{vmatrix}=\begin{vmatrix}x&-y\\2&-1\end{vmatrix}=k - 1$，求实数$k$的取值范围.

答案：
(1) $ \frac{1}{4} $ $ x＞1 $
(2) 由题意，得$ -2 ＜ 4 - mn ＜ 0 $，$ \therefore 4 ＜ mn ＜ 6 $. $ \because m $，$ n $是正整数，$ \therefore mn = 5 $. $ \therefore m = 1 $，$ n = 5 $或$ m = 5 $，$ n = 1 $. $ \therefore m + n = 6 $
(3) 由题意，得$ 3(x - 1) - 2y = -x + 2y = k - 1 $，$ \therefore \begin{cases} 3x - 2y = k + 2 \\ -x + 2y = k - 1 \end{cases} $解得$ \begin{cases} x = \frac{2k + 1}{2} \\ y = \frac{4k - 1}{4} \end{cases} $. $ \because x $，$ y $均为非负数，$ \therefore \begin{cases} \frac{2k + 1}{2} \geqslant 0 \\ \frac{4k - 1}{4} \geqslant 0 \end{cases} $解得$ k\geqslant\frac{1}{4} $. $ \therefore $实数$ k $的取值范围是$ k\geqslant\frac{1}{4} $

13. 对于$x$，$y$，定义一种新运算$T$，规定$T(x,y)=ax + 2by - 1$(其中$a$，$b$均为非零常数). 等号右边是通常的四则运算，例如：$T(0,1)=a\times0 + 2b\times1 - 1 = 2b - 1$.
　　(1)若$T(1,1)=4$，$T(4,-2)=7$，且关于$m$的不等式组$\begin{cases}T(2m,5 - 4m)＜5,\\T(m,3 - 2m)\geq p\end{cases}$恰有4个整数解，求实数$p$的取值范围；
　　(2)若$T(x,y)=T(y,x)$对于任意实数$x$，$y$都成立，则$a$，$b$应满足怎样的关系？

答案：
(1) 由$ T(1,1) = 4 $，$ T(4,-2) = 7 $，得$ \begin{cases} a + 2b - 1 = 4 \\ 4a - 4b - 1 = 7 \end{cases} $解得$ \begin{cases} a = 3 \\ b = 1 \end{cases} $. $ \therefore $易得$ \begin{cases} 6m + 2(5 - 4m) - 1 ＜ 5 \\ 3m + 2(3 - 2m) - 1 \geqslant p \end{cases} $ $ \therefore 2 ＜ m \leqslant 5 - p $. $ \because $不等式组恰有4个整数解，$ \therefore 6\leqslant 5 - p ＜ 7 $，解得$ -2 ＜ p \leqslant -1 $
(2) 由$ T(x,y) = T(y,x) $对于任意实数$ x $，$ y $都成立，得$ ax + 2by - 1 = ay + 2bx - 1 $，即$ (a - 2b)x = (a - 2b)y $总成立，$ \therefore a = 2b $