《2025年通城学典课时作业本八年级数学下册苏科版江苏专版》

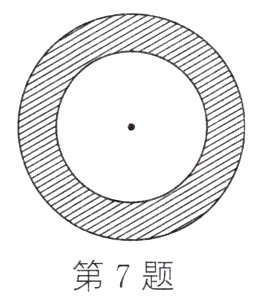
7. 小红和小明在操场做游戏，他们先在地上画了半径分别为2 m和3 m的同心圆（如图），蒙上眼在一定距离外向圈内掷小石子. 若掷中阴影，则小红胜，否则小明胜，未掷入圈内不算.
（1）这个游戏公平吗？为什么？
（2）游戏结束，小明边走边想：反过来，能否用频率估计概率的方法来估算某一不规则图形的面积呢？请设计一个方案解决这个问题（画出图形并补充完整，说明设计步骤、原理，写出估算公式）.

答案：

(1) 这个游戏不公平
∵P(掷中阴影)=$\frac{3^{2}\pi - 2^{2}\pi}{3^{2}\pi}=\frac{5}{9}$，即小红的胜率为$\frac{5}{9}$，
∴小明的胜率为$1 - \frac{5}{9}=\frac{4}{9}$．
∵$\frac{5}{9}\neq\frac{4}{9}$，
∴这个游戏不公平
(2) 能用频率估计概率的方法来估算某一不规则图形的面积 设计方案不唯一，如①设计一个可测量面积的规则图形，如正方形，其面积为S，将不规则图形围起来，如图. ②蒙上眼往正方形中随意掷小石子，掷在正方形外的不计.
③当掷入正方形中的次数充分大(如1万)时，统计结果，设掷入正方形内m次，其中n次掷入不规则图形内. ④设不规则图形的面积为$S_{1}$. 用频率估计概率，即频率P'(掷入不规则图形内)=$\frac{n}{m}\approx$概率P(掷入不规则图形内)=$\frac{S_{1}}{S}$.
∴$\frac{n}{m}\approx\frac{S_{1}}{S}$，即$S_{1}\approx\frac{nS}{m}$