第20页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
1.(2024·云南)某中学为了丰富学生的校园体育锻炼生活,决定根据学生的兴趣爱好采购一批体育用品供学生课后锻炼使用.学校数学兴趣小组为给学校提出合理的采购意见,随机抽取了该校100名学生,了解他们喜欢的体育项目,将收集的数据整理,绘制成如图所示的统计图(该校每名学生被抽到的可能性相等,每名被抽样调查的学生选择且只选择一种喜欢的体育项目).若该校共有学生1000名,则该校喜欢跳绳的学生大约有________名.


答案:
120
2.(2023·鄂州改编)某大学农学院的学生为了解试验田杂交水稻秧苗的长势,从中随机抽取样本对苗高进行了测量,将统计结果(数据四舍五入取整)绘制成如图所示的两幅尚不完整的统计图.
(1)本次抽取的样本水稻秧苗共________株;
(2)求样本中苗高为17cm的水稻秧苗的株数,并补全折线统计图;
(3)根据统计数据,若苗高大于或等于15cm视为优良秧苗,请你估计该试验田90000株水稻秧苗中达到优良等级的株数.

(1)本次抽取的样本水稻秧苗共________株;
(2)求样本中苗高为17cm的水稻秧苗的株数,并补全折线统计图;
(3)根据统计数据,若苗高大于或等于15cm视为优良秧苗,请你估计该试验田90000株水稻秧苗中达到优良等级的株数.

答案:
(1) 500
(2)
∵苗高为14 cm的水稻秧苗的株数为500×20% = 100,
∴苗高为17 cm的水稻秧苗的株数为500 - 40 - 100 - 80 - 160 = 120. 补全折线统计图如图所示
(3) 90000×$\frac{500-(40 + 100)}{500}$ = 64800(株),
∴估计该试验田90000株水稻秧苗中达到优良等级的株数为64800

(1) 500
(2)
∵苗高为14 cm的水稻秧苗的株数为500×20% = 100,
∴苗高为17 cm的水稻秧苗的株数为500 - 40 - 100 - 80 - 160 = 120. 补全折线统计图如图所示
(3) 90000×$\frac{500-(40 + 100)}{500}$ = 64800(株),
∴估计该试验田90000株水稻秧苗中达到优良等级的株数为64800

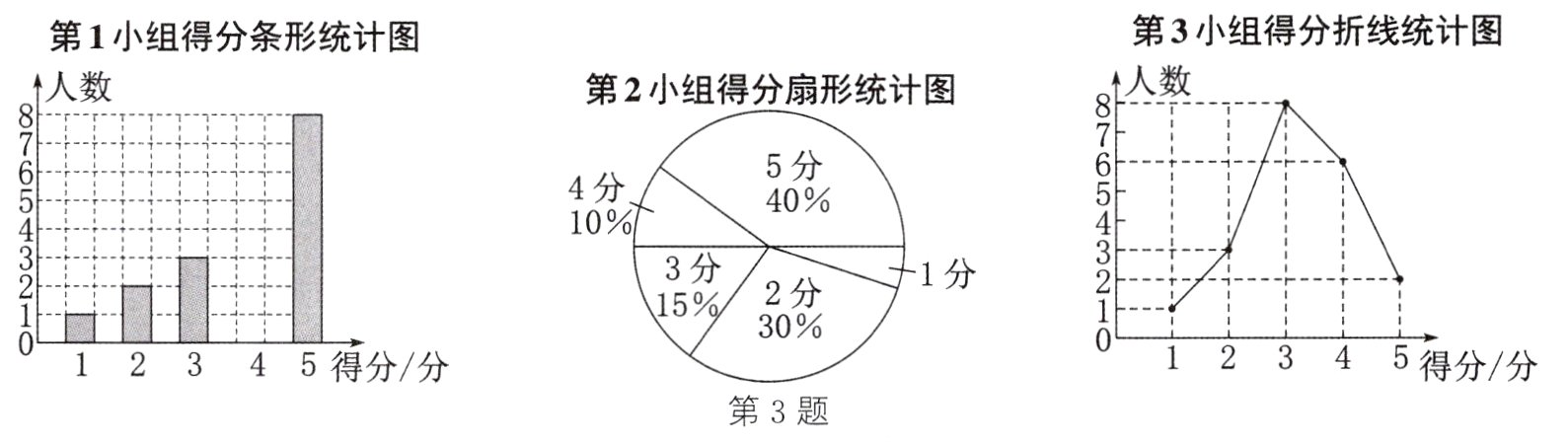
3.(2024·大庆)某中学组织学生参加了国防知识竞赛,将学生的百分制成绩x(分)用5级记分法呈现:“x<60”记为1分,“60≤x<70”记为2分,“70≤x<80”记为3分,“80≤x<90”记为4分,“90≤x≤100”记为5分.现随机将全校学生以20人为一组进行分组,并从中随机抽取了3个小组的学生成绩进行整理,绘制了如下统计表和如图所示的统计图.
| |平均数/分|中位数/分|众数/分|
| ---- | ---- | ---- | ---- |
|第1小组|3.9|4|a|
|第2小组|b|3.5|5|
|第3小组|3.25|c|3|
请根据以上信息,完成下列问题:
(1)①第2小组得分扇形统计图中,“得分为1分”这一项所对应的圆心角度数为________;
②请补全第1小组得分条形统计图.
(2)a=________,b=________,c=________;
(3)已知该校共有4200名学生,以这3个小组的学生成绩作为样本,请你估计该校有多少名学生的成绩不低于90分.

| |平均数/分|中位数/分|众数/分|
| ---- | ---- | ---- | ---- |
|第1小组|3.9|4|a|
|第2小组|b|3.5|5|
|第3小组|3.25|c|3|
请根据以上信息,完成下列问题:
(1)①第2小组得分扇形统计图中,“得分为1分”这一项所对应的圆心角度数为________;
②请补全第1小组得分条形统计图.
(2)a=________,b=________,c=________;
(3)已知该校共有4200名学生,以这3个小组的学生成绩作为样本,请你估计该校有多少名学生的成绩不低于90分.


答案:
(1) ① 18° 解析:360°×(1 - 30% - 15% - 10% - 40%) = 360°×5% = 18°.
② 第1小组中,得分为4分的人数为20 - 1 - 2 - 3 - 8 = 6,补全条形统计图如图所示
(2) 5 3.5 3 解析:第1小组得分出现次数最多的是5分,
∴第1小组得分的众数是5分,即a = 5. 第2小组得分的平均数为1×5% + 2×30% + 3×15% + 4×10% + 5×40% = 3.5(分),即b = 3.5. 将第3小组20名学生的得分从小到大排列,处在中间位置的两个得分的平均数为$\frac{3 + 3}{2}$ = 3(分),
∴中位数是3分,即c = 3.
(3) 20×40% = 8(名),4200×$\frac{8 + 8 + 2}{20 + 20 + 20}$ = 1260(名).
∴估计该校有1260名学生的成绩不低于90分

(1) ① 18° 解析:360°×(1 - 30% - 15% - 10% - 40%) = 360°×5% = 18°.
② 第1小组中,得分为4分的人数为20 - 1 - 2 - 3 - 8 = 6,补全条形统计图如图所示
(2) 5 3.5 3 解析:第1小组得分出现次数最多的是5分,
∴第1小组得分的众数是5分,即a = 5. 第2小组得分的平均数为1×5% + 2×30% + 3×15% + 4×10% + 5×40% = 3.5(分),即b = 3.5. 将第3小组20名学生的得分从小到大排列,处在中间位置的两个得分的平均数为$\frac{3 + 3}{2}$ = 3(分),
∴中位数是3分,即c = 3.
(3) 20×40% = 8(名),4200×$\frac{8 + 8 + 2}{20 + 20 + 20}$ = 1260(名).
∴估计该校有1260名学生的成绩不低于90分

查看更多完整答案,请扫码查看


