《2025年通城学典课时作业本八年级数学下册苏科版江苏专版》

9. 计算$\sqrt{2}\times\sqrt{6}$的结果为_______，这个数落在了如图所示的数轴上的_______段（填序号）.

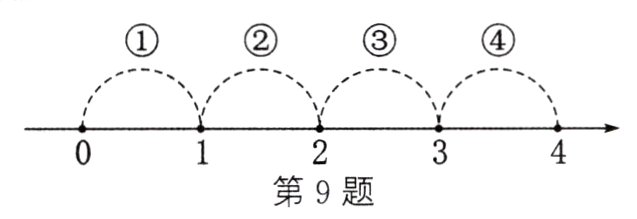
答案： $2\sqrt{3}$ ④

10. 化简：
（1）$\frac{\sqrt{5}}{\sqrt{40}}$； （2）$\sqrt{\frac{18}{a}}(a＞0)$；
（3）$\sqrt{\frac{9y}{8x}}(x＞0,y\geq0)$； （4）$\frac{\sqrt{3a}}{\sqrt{54ab}}(a＞0,b＞0)$；
（5）$\sqrt{\frac{5(a - b)}{27(a + b)}}(a\geq b＞0)$； （6）$\frac{m - n}{\sqrt{m - n}}(m＞n)$.

答案：
(1) $\frac{\sqrt{2}}{4}$
(2) $\frac{3\sqrt{2a}}{a}$
(3) $\frac{3\sqrt{2xy}}{4x}$
(4) $\frac{\sqrt{2b}}{6b}$
(5) $\frac{\sqrt{15a^{2}-15b^{2}}}{9a + 9b}$
(6) $\sqrt{m - n}$

11. 计算：
（1）$9\sqrt{\frac{1}{48}}\div(-\frac{3}{2}\sqrt{2\frac{1}{4}})\times3\sqrt{1\frac{1}{2}}$； （2）$\frac{1}{b}\sqrt{ab^{5}}\cdot(-\frac{1}{2}\sqrt{a^{3}b})\cdot2\sqrt{\frac{1}{b}}(a＞0,b＞0)$.

答案：
(1) 原式$=9\sqrt{\frac{1}{48}}\div(-\frac{3}{2}\sqrt{\frac{9}{4}})\times3\sqrt{\frac{3}{2}}=9\times(-\frac{2}{3})\times3\times\sqrt{\frac{1}{48}\times\frac{4}{9}\times\frac{3}{2}}=-18\times\frac{\sqrt{2}}{12}=-\frac{3\sqrt{2}}{2}$
(2) $\frac{1}{b}\sqrt{ab^{5}}\cdot(-\frac{1}{2}\sqrt{a^{3}b})\cdot2\sqrt{\frac{1}{b}}=(-\frac{1}{b}\times\frac{1}{2}\times2)\cdot\sqrt{ab^{5}\cdot a^{3}b\cdot\frac{1}{b}}=-\frac{1}{b}\sqrt{a^{4}b^{5}}=-a^{2}b\sqrt{b}$